前項では2つのベクトルの合力を扱いましたが、これは2つのベクトルの和(足し算)として表されます。2つであれば前項で説明したように平行四辺形を描いて、その対角線が和になります。
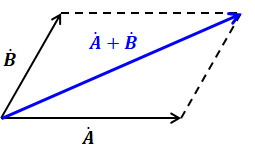
しかし、3つ以上のベクトル和では対角線という考え方が難しいので、次のように考えます(この考え方は、2つのベクトル和のときでも使えます)。
まず、下図のように適当なところに矢印Aを描き、Aの終点をBの起点として矢印Bを延ばします。続いて、Bの終点をCの起点として矢印Cを描きます。以下、矢印DやEがあれば同様に繰り返します。
そうして全ての矢印を描いたら、最初の矢印の起点と、最後の矢印の終点とを結んだ矢印が、ベクトル和に相当します。
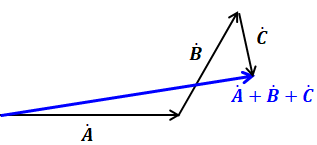
一方、ベクトルの差は、以下のように表すことができます。
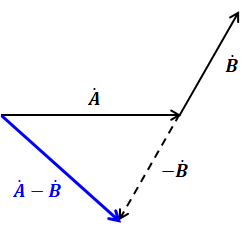
上図を見てもわかるように、ベクトルAからベクトルBを引くときは、まず矢印Aを描き、その終点から、今度は矢印Bの反対方向に同じ大きさの矢印を描きます。つまり、「A-B」という引き算を、「A+(-B)」という足し算のように考えるとわかりやすいかもしれません。-Bというベクトルは、Bと大きさが同じで、向きが真逆のベクトルとなります。
ベクトルの数が3つ以上になっても同様に、マイナスの記号が付いたベクトルは反対に進むと考えることができます。たとえば、4つのベクトルの和と差が混在している例「A-B-C+D」だと以下のように描くことができます。
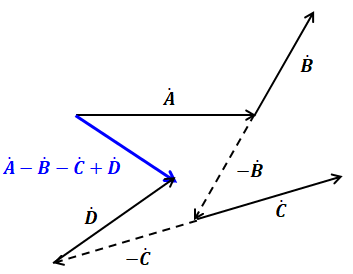

コメント