問 題
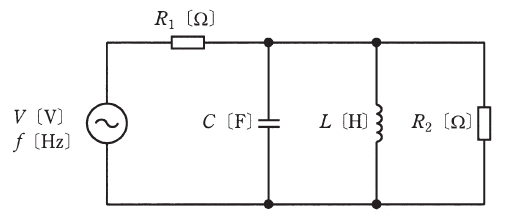
図のように、R1=20[Ω]とR2=30[Ω]の抵抗、静電容量![]() のコンデンサ、インダクタンス
のコンデンサ、インダクタンス![]() のコイルからなる回路に周波数f[Hz]で実効値V[V]が一定の交流電圧を加えた。f=10[Hz]のときにR1を流れる電流の大きさをI10Hz[A]、f=10[MHz]のときにR1を流れる電流の大きさをI10MHz[A]とする。
のコイルからなる回路に周波数f[Hz]で実効値V[V]が一定の交流電圧を加えた。f=10[Hz]のときにR1を流れる電流の大きさをI10Hz[A]、f=10[MHz]のときにR1を流れる電流の大きさをI10MHz[A]とする。
このとき、電流比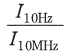 の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.4
- 0.6
- 1.0
- 1.7
- 2.5
解 説
まず、問題文に与えられた数値を使ってコイルとコンデンサそれぞれのリアクタンスXL10HzとXC10Hzを求めます。
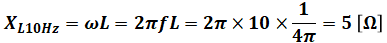
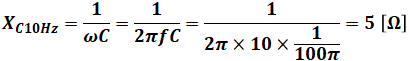
よって、2つのリアクタンスは同じ大きさになります。コイルとコンデンサが並列に並んでいるとき、その合成リアクタンスは和で表すことができますが、コイルとコンデンサではリアクタンスの符号が反対なので、今回はちょうど打ち消し合って合計0となります(余談ですが、これを並列共振状態といいます)。
つまり、f=10[Hz]のときはコイルとコンデンサには電流が流れないので、R1とR2が直列に並んだ回路となり、そこを流れる電流I10Hzは次のように計算することができます。
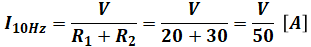
続いて、f=10[MHz]のときを考えます。このときのコイルとコンデンサそれぞれのリアクタンスXL10MHzとXC10MHzは次の通りです。
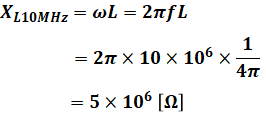
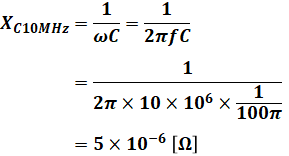
よって、XC10MHzはR2やXL10MHzと比べて極端に小さいので、R1を流れる電流はその後、抵抗R2やコイルを流れることなく、ほぼ全ての電流がコンデンサを流れます。つまり、この場合の回路は次のように描くことができます。
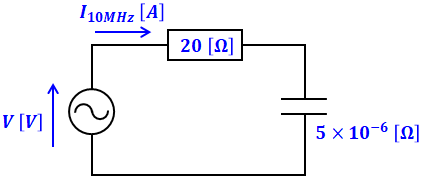
ここで、XC10MHzはR1と比べてもはるかに小さいため、I10MHzを計算する際はR1のみを使った近似式で問題ありません(もちろん、XC10MHzを含めて計算しても構いませんが、計算が煩雑になります)。

以上から、求める答えは以下のように計算できます。
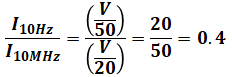

コメント