以下の図のように、入力信号と出力信号との論理演算を図式化したものを論理回路といいます。
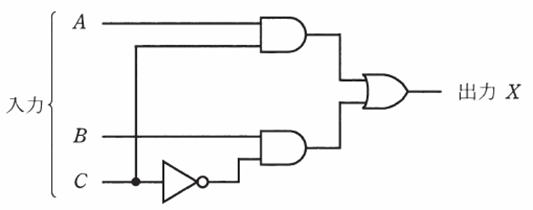
この図では入力信号にはA、B、Cの3種類ありますが、それぞれの入力はONかOFF、つまり1か0の入力となります。たとえば、入力が「A=1、B=0、C=0」のとき、出力Xは1なのか、それとも0なのか、ということをこの論理回路から読み取ることができます。
そのために、まずは論理回路に使われる基本的な記号の意味を知る必要があるので、この項ではそれらの記号を紹介し、具体的な入力と出力の関係については次項で解説します。
NOT
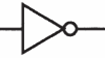
この記号は「NOT」を表しています。
信号は普通、左(入力側)から右(出力側)へと進み、入力が0のときは1として出力します。反対に、入力が1のときは0として出力します。
(入力、出力)=(0,1)、(1,0)
AND
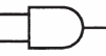
この記号は「AND」を表しています。
入力の線が2つありますが、「AND」では入力が2つとも1のときだけ、出力も1になります。言い換えれば、入力が片方でも0なら、出力は0になります。
(入力①、入力②、出力)=(0,0,0)、(0,1,0)、(1,0,0)、(1,1,1)
ちなみに、入力が3つ(またはそれ以上)になることもありますが、3つのときは、全て入力が1のときだけ出力も1となり、複数の入力のうち1つでも0があると、出力も0となります。
OR
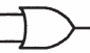
この記号は「OR」を表しています。
「OR」は「AND」と比較するとわかりやすいですが、「AND」は入力の全てが1のときだけ出力も1になるのに対して、「OR」は入力が1つでも1なら、出力が1になります。つまり、「OR」の出力が0になるのは、入力が全て0だったときだけです。
(入力①、入力②、出力)=(0,0,0)、(0,1,1)、(1,0,1)、(1,1,1)
NAND
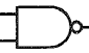
「AND」の出力側に「○」が付いているものを「NAND」と呼びますが、これは「AND」と「NOT」を合わせたものです。
考え方としては、まずは「AND」と同様に考えて、その出力結果を反対に(「NOT」に)するというものです。つまり、出力の結果は「AND」のときと真逆になります。
(入力①、入力②、出力)=(0,0,1)、(0,1,1)、(1,0,1)、(1,1,0)
NOR
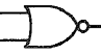
「OR」の出力側に「○」が付いているものを「NOR」と呼びますが、これは「OR」と「NOT」を合わせたものです。
考え方は「NAND」のときと同様ですが、「OR」の出力結果を反対に(「NOT」に)するというものです。つまり、出力の結果は「OR」のときと真逆になります。
(入力①、入力②、出力)=(0,0,1)、(0,1,0)、(1,0,0)、(1,1,0)
EX-OR
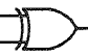
これは「OR」に似ていますが、排他的論理和はいい、「EX-OR」と略されます。
意味合いとしては、2つの入力のどちらか一方が1のときだけ出力も1となるというものです。入力が2つとも0だと出力も0になるのは「OR」と同様ですが、入力が2つとも1であっても出力が0になるのが特徴です。
(入力①、入力②、出力)=(0,0,0)、(0,1,1)、(1,0,1)、(1,1,0)
ちなみに、出題頻度はあまり高くありませんが、「EX-OR」の記号の出力側に○が付くと、排他的否定論理和「EX-NOR」となります。これは「EX-OR」の出力結果を逆さまにしたものです。
以上が論理回路の基本的な記号になります。これらを踏まえて、次項では論理回路全体の入力と出力について考えていきたいと思います。

コメント