直線上の光源
前項では点光源があるときの照度について考えましたが、今度は点光源ではなく、線光源(無限直線上の光源)の場合を扱います。イメージとしては以下の図のような感じです。
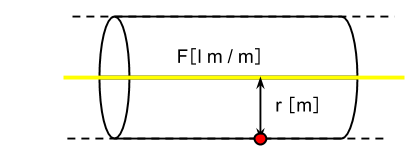
上図の黄色い線が光源だと思ってください。このような場合、ある点(上図の赤い点)での照度は、次の式で表されます。
![]()
ここで、面積Aが2πrになっていますが、これは円周の長さに相当します。
考え方としては、光源上のある1点から発せられる光束が、その周囲の円に均等に行き渡るというものです。実際には光源上の1点から発せられる光束は斜めにも飛んで行くので、全ての光束が赤い点を含む円に届くわけではないのですが、光源上の別の点からの光束についても、その一部が上図の赤い点のところに飛んできます。
よって、正味として、光源のある点がその周囲だけに照射されることと同じになるので、上式のように面積Aのところは2πrでいいことになります。
球形光源
光源が点光源でも線光源でもなく、大きさを持つ光源(たとえば球形光源)が出題されることもあります。もちろん大きさを持つ光源自体には様々な形がありますが、大体は球形をしている場合が多いので、ここでは球形光源として扱います。
結論を先に示しておくと、球形光源では、光束発散度M[lm/m2]と輝度L[cd/m2]との間に以下の式が成り立ちます。
![]()
以下にこの式の導出を示しますが、式自体を覚えておけば話が早いので、これは公式として押さえておきたいところです。
まず、光束発散度の基本式は照明の記号と単位(その他)のページでも紹介した通り、
![]()
で表され、分子の光束F[lm]は、同上のページの光度I[cd]のところで解説しているように、
![]()
となります。
さらに、立体角ω[sr]は、照明の記号と単位(立体角)のページで扱っていて、表面積は球なので4πr2となり、
![]()
で表されます。
一方、最初の式(光束発散度Mの式)の分母であるAは球形光源の表面積なので4πr2となります。
以上を次々に代入していくと、次のような計算ができます。
![]()
ここで、これも照明の記号と単位(その他)のページを参照してもらいたいのですが、光度I[cd]は輝度L[cd/m2]と観測点から光源を見たときの見かけの面積A'[m2]を使うと、
![]()
となります。
ちなみに、ここでのA’は球形光源の表面積ではなく、観測地点での光源の見かけの面積、つまり、たとえば光源が天井にあったとき、地面に映る影の面積のことです。そのため、A’は半径がrの円の面積なので、πr2となります。
これを先ほどの式に代入すると、
![]()
となって、冒頭に示した公式が得られます。
以上のようにいくつもの式を組み合わせて初めて導出できるので、これはもう公式として覚えてしまうのが現実的かもしれません。

コメント