照明の記号と単位(立体角)

照明に関する記号は数が多く、その名前も似ているものが多いので紛らわしいです。しかし、これらを正確に記憶しておかないと照明の計算問題を解く際に困るので、このページと次のページで用語と記号、単位を紹介します。

紹介する変数は全部で以下の7つありますが、このページではそのうちの立体角について扱います。

1. 立体角ω [sr]
2. 光束F [lm]
3. 光度I [cd]
4. 照度E [lx]
5. 輝度L [cd/m²]
6. 光束発散度M [lm/m²]
7. 光量Q [lm・s]

立体角ω [sr]

最初に紹介するのが「立体角」です。

これは、ある点からの空間的な広がりを表す変数で、記号はωで表され、その単位は[sr]です。ステラジアンと読みます。ωは以下の式から求めることができます。

• ω：立体角[sr]
• S：光源の表面積[m²]
• r：光源の中心から表面までの距離[m]

たとえば、球形光源の場合は、光源の表面積が4πr²となるので、立体角ωは次のように計算できます。

一方、円板光源(厚さは無視)であれば、光源の表面積がπr²となるので、立体角ωは次のように計算できます。

また、より一般論として考える場合は、下の図をみてください。

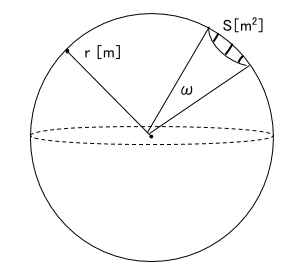
上図のように、ある点を中心とした半径r[m]の球を考えて、その球を切り取る面積をS[m²]とします。そのときの中心点からの広がり具合が、立体角ω[sr]ということになります。

また、下図のように平面角(普通の角度)をθ[°]とすると、ωを別の表し方ができます。

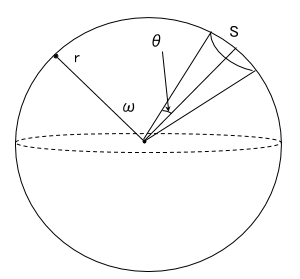
このθを使う式が出題されることもよくあるので、これらの式は覚えておくとよいと思います。