前項ではエレベータの昇降に使用する電動機の出力の計算式を解説しましたが、電動機で駆動するポンプを用いて水を揚水する際の電動機の出力に関する計算問題も多く出題されています。
エレベータで荷物を持ち上げるのも、ポンプで水を揚げるのも原理は変わらないので、基本的には同じ考え方で解くことができます。つまり、ポンプによる揚水で使う電動機の出力P[W]は、移動した水の位置エネルギーに相当するということです。
ただし、出力は全く位置エネルギーと等しくなるわけではなく、いくつか注意点があります。まずは覚えておきたい公式を以下に示し、その下でそれぞれの注意点について解説していきます。
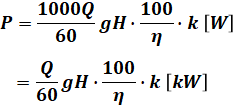
- P:電動機の出力[W]
- Q:毎分の揚水量[m3/min]
- g:重力加速度9.8[m/s2]
- H:全揚程(実揚程に損失水頭を加えた高さ)[m]
- η:効率[%]
- k:余裕係数
まず、位置エネルギーといえばMgHですが、この質量Mにあたる部分が今回は1000Q/60というややこしい数字になっています。1000で掛けているのは、問題文で揚水量の単位が[m3/min]と与えられることが多いので、[m3]→[kg]に変換するためです。また、60で割っているのは、[min]→[s]に変換するためです。
このように、SI単位系で使われる単位([kg]や[s])に直しておかないと、計算結果の単位が[W]と合わなくなります。
続いて、高さHは単純に水を揚げた高さ(=実揚程)ではなく、それに損失水頭を加えた実揚程とする必要があります。たとえば、実揚程が100[m]で損失水頭が1[m]なら、全揚程は101[m]となります。
また、揚水ポンプの電動機は効率100%では仕事ができないので、それを加味しなければなりません。これは前項のエレベータの昇降でも同じでした。問題によって「効率」または「全体の効率」として1つの数値が与えられている場合と、「ポンプの効率」と「電動機の効率」として2つの数値が与えらえる場合があります。
たとえば全体の効率が80%とあれば、出力の基本式を0.8で割れば良く、ポンプの効率が80%で電動機の効率が90%とあれば、0.8×0.9=0.72なので、0.72で割る必要があります。
最後に、ポンプの設計や工作上の誤差というものがどうしても少し生じてしまうので、普通はその誤差を見込んで余裕をもたせた電動機を使います。つまり、電動機の出力は、必要量に余裕係数(普通は1.1とか1.2くらい)を掛けた分だけ必要ということです。ただし、問題文で余裕係数について触れていなければ、特に気にしなくて大丈夫です。

コメント