直流発電機の誘導起電力

直流発電機の項目でぜひ覚えてもらいたい公式が一つあります。それは、電機子の誘導起電力の式で、以下の式で表すことができます。誘電起電力や式の導出についてもこの項で解説しますが、とにかくこの式を覚えておくことが重要です。

• E：電機子の誘導起電力[V]
• p：磁極数
• Z：電機子総導体数
• a：巻線の並列回路数
• Φ：1極あたりの磁束[Wb]
• n：電機子の回転速度[min^-1]

以上でこの項の内容はほぼ終わりなので、以下は参考までに軽い気持ち読んでください。

直流発電機は、フレミングの右手の法則に従って動きます。フレミングの右手の法則とは、長さl[m]の導体を磁束密度B[T]の磁束の方向と直角に置き、速度v[m/s]で導体と磁束の両方に直角な方向に移動させると、導体にe=Blv[V]の誘導起電力が発生するという法則です。

右手の親指と人差し指と中指をそれぞれ垂直方向となるようにしたとき、それぞれの指と上記の各パラメータの向きが次のように対応することから、フレミングの右手の法則という名が付いています。

• 中指：誘導起電力eの向き(それに伴い生じる電流の向き)
• 人差し指：磁界Bの向き
• 親指：導体の速度vの向き(導体を動かす向き)

以上から、この原理で動いている直流発電機の電機子にも、誘導起電力が発生します。1極あたりの磁束がΦ[Wb]、磁極数がp、電機子総導体数がZ、巻線の並列回路数がa、電機子の直径がD[m]である直流機が回転速度n[min^-1]で回転しているとき、その周辺速度は次の式で表すことができます。

そして、直流機の正負のブラシ間にはZ/a本の導体が直列に接続されるので、電機子の誘導起電力は、

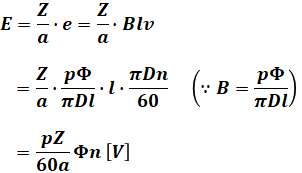
と計算することができます。これが冒頭の公式です。