電験三種 R5年度下期 機械 問18 問題と解説

　問 題　　　　　

図1は、調節計の演算回路などによく用いられるブロック線図を示す。次の(a)及び(b)の問に答えよ。

(a)　図2は、図1のブロックG₁(jω)の詳細を示し、静電容量C[F]と抵抗R[Ω]からなる回路を示す。

この回路の入力量V₁(jω)に対する出力量V₂(jω)の周波数伝達関数を表す式として、正しいものを次の(1)～(5)のうちから一つ選べ。

(b)　図1のブロック線図において、閉ループ周波数伝達関数で、ゲインKが非常に大きな場合の近似式として、正しいものを次の(1)～(5)のうちから一つ選べ。

なお、この近似式が成立する場合、この演算回路は比例プラス積分要素と呼ばれる。

 

 

 

 

 

　解 説　　　　

(a)

問われているのはV₁(jω)とV₂(jω)の比です。各選択肢にはいずれも「CR」が含まれているので、まずはV₁(jω)とV₂(jω)のそれぞれを、CやRを使った式として表すことを目指します。

図2のうち入力電圧に注目すると、RとCが直列に並んでいるため、入力電圧V₁(jω)は、電流I(jω)を使って次のように表すことができます。

一方、出力電圧に注目すると、こちらにはRしかないため、出力電圧V₂(jω)は、電流I(jω)を使って次のように表されます。

(1)式と(2)式から、は以下のように計算できます。

よって、正解は(5)となります。

(b)

本問のようなフィードバック制御系の伝達関数はブロック線図の中でも重要かつ頻出なので、ぜひ押さえておきたい内容です。

下図の左側のようなフィードバックモデルは右側のように簡略化できるので、入力をX(s)、出力をY(s)として式化すると次のようになります。これは最重要公式の一つとして覚えておいてください。なお、図中の「∓」が、式では「±」とひっくり返ることに注意が必要です。

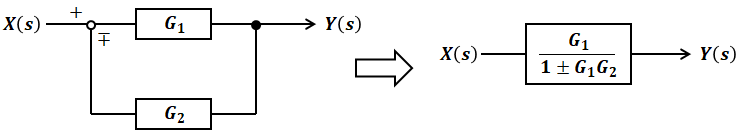
上記を今回の問題に当てはめて描き直すと、以下のように表すことができます。

ここで、本問ではが問われているので、これに上記の(4)式を代入すると、次に示す(5)式のようになります。

この(5)式に対して、設問(a)で求めた(3)式を代入すると、以下の(6)式のように表すことができます。

この(6)式が一応の答えですが、二重分数であり選択肢のどれにも当てはまらないので、選択肢のいずれかに合うように計算を進めていくと、次のようになります。なお、問題文に「ゲインKが非常に大きな場合の近似式」とある点に注意してください。

以上から、正解は(3)です。