問 題
図に示すようなフィードバック制御系がある。閉ループ周波数伝達関数
のボード線図の折線近似ゲイン特性として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、ωは角周波数[rad/s]を表す。
解 説
本問のようなフィードバック制御系の伝達関数はブロック線図の中でも重要かつ頻出なので、ぜひ押さえておきたい内容です。
下図の左側のようなフィードバックモデルは右側のように簡略化できるので、入力をX(s)、出力をY(s)として式化すると次のようになります。これは最重要公式の一つとして覚えておいてください。なお、図中の「∓」が、式では「±」とひっくり返ることに注意が必要です。
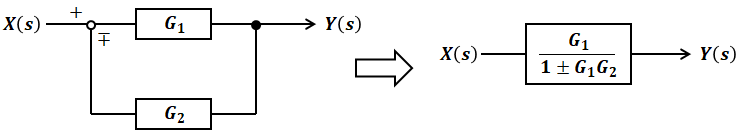
続いて、今回の問題にこれを適用していくと、まず上記のX(s)のところはR(jω)で、Y(s)のところはC(jω)です。
そして、上記のG1のところには「K」と「1/jωT」が直列に並んでいるため、G1はこれらの積となります。つまり、「G1＝K/jωT」です。また、G2の位置にはブロックが何もないので、「G2＝1」となります。
よって、このフィードバック制御系の伝達関数は、次の(2)式のように表されます。
次に確認しておきたいのは、ゲイン特性は以下の(3)式で表されるということです。この式も重要公式として覚えておく必要があります。
なお、本問はこのゲイン特性をグラフ化したものとして、正しいグラフ(ボード線図)を選ぶ問題となります。そこで、(3)式に(2)式を代入すると、次に示す(4)式のようになります。
上式は曲線となりますが、本問では折線近似ゲイン特性を用いることが問題文に明記されています。これは、本来曲線であるものを、折れ点角周波数を境に2つの直線として近似できるということを表しています。
2直線の境界となる「折れ点角周波数」は、(4)式において実部と虚部の大きさが等しくなるωの値をとる点です。つまり、次の(5)式のように計算できます。
よって、折れ点角周波数がω＝K/Tだとわかったので、この時点で選択肢(4)または(5)が正解候補となります。あとは両者の違いに注目し、たとえばω＝0のときのゲインgを(4)式を使って算出すれば、選択肢(4)と(5)のどちらが正しいか判断できます。
(6)式より、ω＝0のとき、ゲインg(グラフの切片)＝0となるので、選択肢(4)と(5)では、選択肢(4)のほうが正しいと判断することができます。
以上から、正解は(4)となります。
コメント