電験三種 R5年度下期 理論 問12 問題と解説

　問 題　　　　　

次の文章は、真空中における電子の運動に関する記述である。

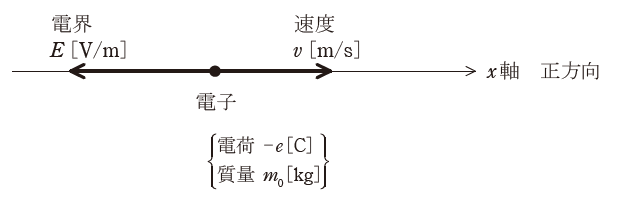
図のように、x軸上の負の向きに大きさが一定の電界E[V/m]が存在しているとき、x軸上に電荷が－e[C](eは電荷の絶対値)、質量m₀[kg]の1個の電子を置いた場合を考える。

x軸の正方向の電子の加速度をa[m/s²]とし、また、この電子に加わる力の正方向をx軸の正方向にとったとき、電子の運動方程式は

m₀a＝(　ア　)　…　①

となる。①式から電子は等加速度運動をすることがわかる。したがって、電子の初速度を零としたとき、x軸の正方向に向かう電子の速度v[m/s]は時間t[s]の(　イ　)関数となる。

また、電子の走行距離x_dis[m]は時間t[s]の(　ウ　)関数で表される。さらに、電子の運動エネルギーは時間t[s]の(　エ　)で増加することがわかる。

ただし、電子の速度v[m/s]はその質量の変化が無視できる範囲とする。

上記の記述中の空白箇所(ア)～(エ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

• (ア)　　(イ)　　(ウ)　　(エ)

1. eE　　　一次　　二次　　1乗
2. eE/2　　二次　　一次　　1乗
3. eE²　　  一次　　二次　　2乗
4. eE/2　　二次　　一次　　2乗
5. eE　　　一次　　二次　　2乗

 

 

 

 

 

　解 説　　　　

まず、①の式は電子の運動方程式なので、右辺の(　ア　)には電子に働く力、つまり静電気力F[N]が入ります。

静電気力F[N]は、電荷－e[C]と電界－E[V/m]との積で表すことができるので、電子の運動方程式は次のように表すことができます(電界にマイナスを付けているのは、この電子に加わる力(静電気力)の正方向をプラスとしているためです。問題の図を見てわかる通り、電子の運動方向(静電気力の向き)と電界の向きとは反対になります)。

• m₀：電子の質量 [kg]
• a：電子の加速度 [m/s²]
• e：電子の電荷 [C]
• E：電界 [V/m]

よって、(　ア　)には「eE」が入ります。

続いて、問題文には「①式から電子は等加速度運動をすることがわかる」とさらっと書かれていますが、念のため、これについて少し詳しく解説しておきます。

(1)式を加速度aについて解くと、次に示す(2)式のようになります。

(2)式の右辺のパラメータ(e、E、m₀)は全て定数なので、加速度aはconst.(一定)であることがわかります。よって、この電子の運動は等加速度運動であるといえます。

また、等加速度運動であることがわかれば、速度v[m/s]は時間t[s]を使って次の(3)式のように表すことができます。なお、問題文より初速度v₀=0です。

よって、電子の速度v[m/s]は時間t[s]の一次関数となるので、(　イ　)には「一次」が入ります。

同様に、等加速度運動の距離x_dis[m]と時間t[s]の関係は、以下の(4)式の通りとなり、xはtの二次関数となります。

よって、(　ウ　)は「二次」となります。

最後に、電子の運動エネルギーについて考えます。

(　エ　)では電子の運動エネルギーと時間t[s]の関係が問われていますが、電子の運動エネルギーは1/2m₀v²[J]で表すことができます。

ここで、(3)式や(　イ　)から、tとvは一次関数の関係なので、電子の運動エネルギー1/2m₀v²[J]はtの2乗に比例することがわかります。

よって、(　エ　)は「2乗」となります。

以上から、

• (ア)：eE
• (イ)：一次
• (ウ)：二次
• (エ)：2乗

となるので、正解は(5)です。