問 題
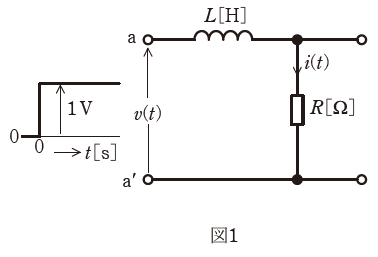
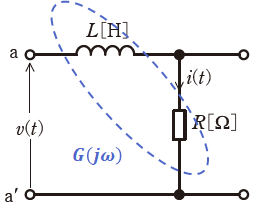
図1に示すR-L回路において、端子a、a’間に単位階段状のステップ電圧v(t)[V]を加えたとき、抵抗R[Ω]に流れる電流をi(t)[A]とすると、i(t)は図2のようになった。
この回路のR[Ω]、L[H]の値及び入力をa、a’間の電圧とし、出力をR[Ω]に流れる電流としたときの周波数伝達関数G(jω)の式として、正しいものを次の(1)~(5)のうちから一つ選べ。

解 説
問われているのはR、L、G(jω)の値なので、まずはRについて考えます。
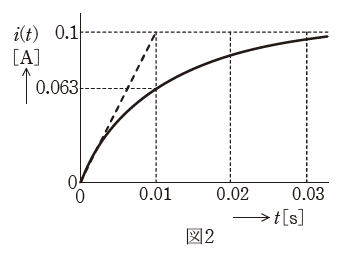
問題文には「ステップ電圧v(t)[V]を加える」とありますが、図1を見ると最終的なv(t)の値は1[V]であることがわかります。一方で、図2より、十分に時間が経ったあとのi(t)の値は0.1[A]となります。
よって、十分に時間が経ったあとはL[H]の影響はなくなるので、Rの値はオームの法則により、次の(1)式のように算出することができます。
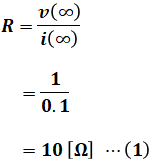
これでRがわかったので、次はLについて考えます。
図2の縦軸では「i(t)=0.063」と「i(t)=0.1」が表記されています。ここで「i(t)=0.063」が強調されているのは、電流が流れ始めてから最大(定常状態)電流の約63.2%になるまでに掛かった時間を「時定数」と定めているからです。
RL直列回路における時定数τの式は、以下のように表すことができます。
![]()
今回の場合、図2よりτ=0.01と読み取れます。よって、(1)式と(2)式より、Lは次のように計算することができます。
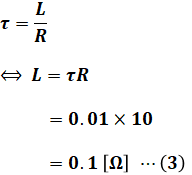
ここまででRとLがわかったので、最後にG(jω)について考えます。
問題文より、入力をv(t)、出力をi(t)としたときの周波数伝達関数がG(jω)とあるので、これら3つの関係式は次のように表すことができます。
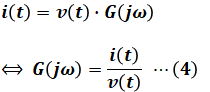
一方で、RとLは直列に並んでいるので、v(t)とi(t)はオームの法則より、次のような関係式で表すこともできます。
![]()
また、(5)式を(4)式に代入し計算を進め、さらに(1)式と(3)式で求めたRとLの値を代入すると、次の(6)式のようになります。
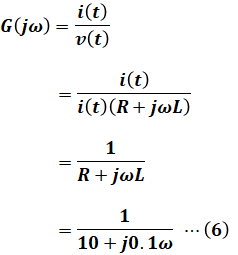
よって、(6)式の結果をG(jω)の答えとしたいのですが、選択肢に該当するものがありません。しかし、よく見ると選択肢(1)のG(jω)だけが、(6)式の結果の分母・分子を10で割った値であることがわかります。その他の選択肢は、このような変形ができませんので、G(jω)は以下の(7)式の通りとなります。
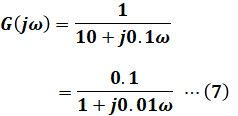
以上の(1)式、(3)式、(7)式より、正解は選択肢(1)となります。

コメント