問 題
定格出力36kW、定格周波数60Hz、8極のかご形三相誘導電動機があり、滑り4%で定格運転している。このとき、電動機のトルク[N・m]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、機械損は無視できるものとする。
- 382
- 398
- 428
- 458
- 478
解 説
この設問では誘導電動機のトルクT[N・m]の値が問われています。誘導電動機のトルクTを表す式は以下の通りですが、これは重要公式として押さえておきたい知識です。
![]()
- T:誘導電動機のトルク [N・m]
- P2:二次入力 [W]
- Ns:同期速度 [min-1]
もしこの(1)式をそのまま暗記することが難しければ、以下の式変換を参考にしてください(上式を覚えられるなら、次の(2)式は特に気にする必要はありません)。
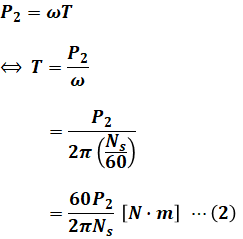
よって、(1)式を計算できれば解決なのですが、現時点では、(1)式に出てくる二次入力P2も同期速度Nsもわかっていません。そのため、これらを計算で求めるのが当面の目標となります。
まずは二次入力P2について考えます。
誘導電動機が滑りsで運転しているとき、二次銅損Pc2の値は、二次入力P2のs倍となります。そのため、下図の通り、二次入力から二次銅損を引いた値が機械出力Pmとなります。

問題文より機械出力(定格出力)Pmは36[kW]であり、滑りは4%(s=0.04)なので、二次入力P2は次のように計算することができます。
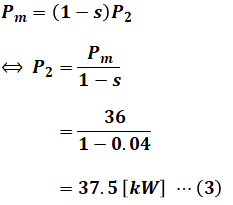
これで二次入力P2がわかったので、続いて、同期速度Nsを求めます。
同期速度Nsは、以下に示す(4)式から求めることができます。これも重要公式の一つとして覚えておいてください。
![]()
- Ns:同期速度 [min-1]
- p:磁極の数 [極]
- f:周波数 [Hz]
よって、問題文で磁極の数pは8極、周波数fは60[Hz]と与えられているため、同期速度Nsは次のように計算することができます。
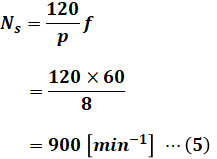
以上から、(3)式と(5)式の結果を(1)式に代入して計算を進めれば、求めたいトルクTを算出することができます。
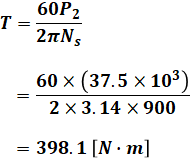
よって、正解は(2)となります。

コメント