問 題
三相3線式高圧配電線の電圧降下について、次の(a)及び(b)の問に答えよ。
図のように、送電端S点から三相3線式高圧配電線でA点、B点及びC点の負荷に電力を供給している。S点の線間電圧は6600Vであり、配電線1線当たりの抵抗及びリアクタンスはそれぞれ0.3Ω/kmとする。
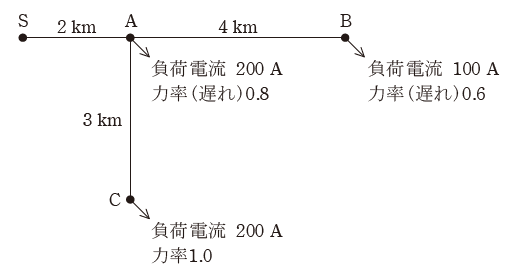
(a) S-A間を流れる電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 405
- 420
- 435
- 450
- 465
(b) A-Bにおける電圧降下率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 4.9
- 5.1
- 5.3
- 5.5
- 5.7
解 説
(a)
問題の図を見ると、各所を流れる電流Iには次のような関係があることがわかります。
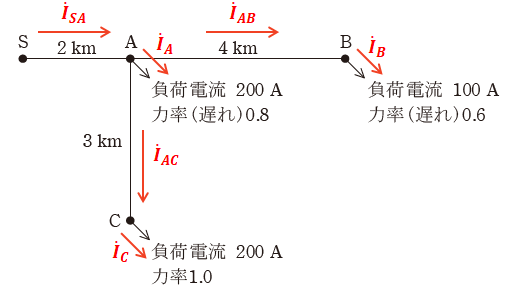
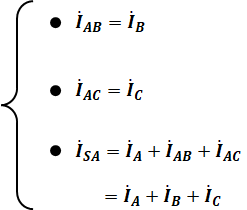
よって、問われている「S-A間を流れる電流の値」は、点A、点B、点Cを流れる電流の合力の大きさとなります。
ここで、各点を流れる電流は、問題の図から以下の(1)~(3)式のように表すことができます。
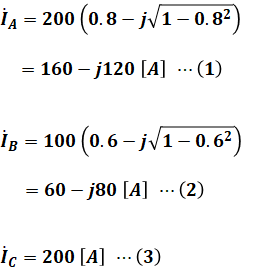
(1)~(3)式より、「S-A間を流れる電流の値」は次のように算出することができます。
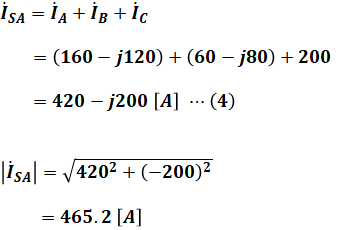
以上から、正解は(5)となります。
(b)
まず、設問(b)では「A-Bにおける電圧降下率」が問われていますが、電圧降下率を算出する際に基準電圧をどこにとるかは注意が必要です。ここを間違えると答えが合わなくなります。
大抵の場合は問題文で「電圧降下率は受電端電圧基準によるものとする」のように明記されていますが、今回はそれがありません。しかし、明記されていない場合でも、受電端電圧を基準にするのが原則であると覚えておいてください。
つまり、今回の場合はB点の電圧を基準とするので、電圧降下率εは下式のように表すことができます。
![]()
- ε:電圧降下率 [%]
- Vd(AB):A-B間での電圧降下 [V]
- VB:受電端電圧(B点での電圧) [V]
上式より、Vd(AB)とVBがわかれば答え(ε)は出せるのですが、それにはA-B間での送電端であるA点における電圧を知る必要があります。
そのため、本問の解法の流れは、次のようになります。
- まずは、S-A間の電圧降下を計算して点Aでの電圧を求めます。
- それから、A-B間の電圧降下を計算して点Bでの電圧を求めます。
- 最後に、上記の(5)式を用いて電圧降下率εを計算します。
ここで、三相3線式送電線における電圧降下の式は、以下のように表すことができます。これは重要公式としてそのまま覚えておきたい知識ですが、もし導出方法を知りたい場合は三相3線式送電線の電圧降下のページを参照してください。
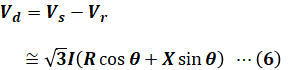
- Vd:電圧降下 [V]
- Vs:送電端電圧 [V]
- Vr:受電端電圧 [V]
- I:線電流 [A]
- R:抵抗(電線1条あたり) [Ω]
- X:リアクタンス(電線1条あたり) [Ω]
- cosθ:負荷の力率
よって、S-A間の電圧降下Vd(SA)は(6)式を使って次のように計算することができます。なお、抵抗とリアクタンスはともに0.3[Ω/km]であるので、S-A間ではそれぞれ0.3×2=0.6[Ω/km]となります。また、以下の計算過程では設問(a)の(4)式を利用しています。
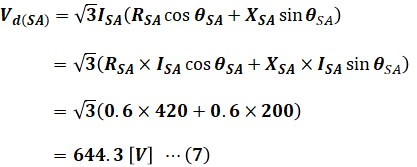
(7)式より、S-A間の電圧降下は644.3[V]であり、S点での電圧は6600[V]なので、点Aでの電圧VAは次のように計算できます。
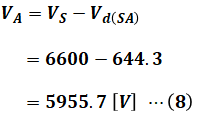
続いて、A-B間の電圧降下Vd(AB)をS-A間のときと同じように(6)式を使って求めます。ここでは線路長が4[km]なので、抵抗とリアクタンスはそれぞれ1.2[Ω]となります。また、計算過程では設問(a)の(2)式を利用しています。
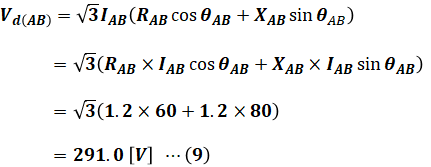
(9)式よりA-B間の電圧降下は291.0[V]であり、A点での電圧は(8)式から5955.7[V]であるので、点Bでの電圧VBは次のように計算できます。
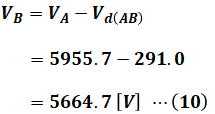
よって、(5)式に(9)式と(10)式を代入すれば、求めたい電圧降下率εを算出することができます。
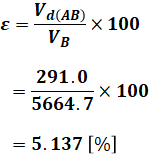
以上から、正解は選択肢(2)となります。

コメント