問 題
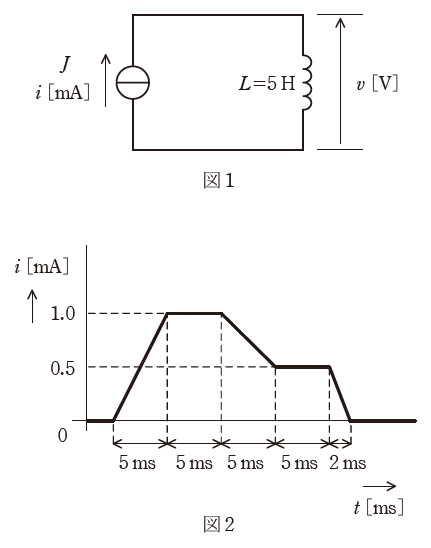
図1のように、インダクタンスL=5Hのコイルに直流電流源Jが電流i[mA]を供給している回路がある。電流i[mA]は図2のような時間変化をしている。このとき、コイルの端子間に現れる電圧の大きさ|v|の最大値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.25
- 0.5
- 1
- 1.25
- 1.5
正解 (4)
解 説
本問のように、静止しているコイルに時間変化する電流が流れると、電磁誘導によってコイルに起電力が生じます(=誘導起電力)。
なお、本問から少し脱線しますが、この起電力の向きも重要です。誘導起電力は、コイル内の磁束の変化を妨げる向きとなるように発生します。
つまり、電流が増加している間は問題の図1に記載されているv[V]の矢印の向きに起電力が生じ、電流が減少している間は反対向きとなります。また、電流が一定の間は起電力は発生しません。(以上、脱線おわり)
ここで、時間変化する電流によって生じる誘導起電力v[V]は、インダクタンスL[H]、電流変化ΔI[A]、時間変化Δt[s]を用いると、次の式で表すことができます。
![]()
本問で問われているのは誘導起電力の大きさ|v|の最大値ですが、Lは5[H]と定数であるため、Δi/Δtの値が最も大きければよいという話になります。
問題の図2のうち、電流変化(Δi/Δt)が最も大きいところに注目すると、傾きが最も大きいのは右端の2[ms]の部分であることがわかります。この2[ms]の間に電流は0.5[mA]だけ減少しているので、(1)式より、誘導起電力の大きさ|v|は次のように計算することができます。
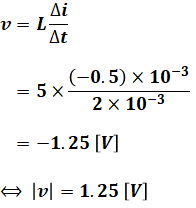
以上から、正解は(4)となります。

コメント