電験三種 R5年度上期 理論 問6 問題と解説

　問 題　　　　　

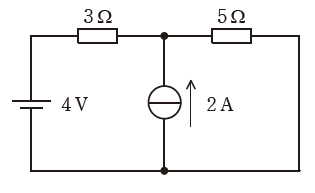
図のような直流回路において、3Ωの抵抗を流れる電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.35
2. 0.45
3. 0.55
4. 0.65
5. 0.75

 

 

 

 

 

　解 説　　　　

この問題のように電源が2つ以上ある回路の計算問題では、重ね合わせの原理を使うと便利です。

重ね合わせの原理とは、電源が複数ある電気回路において、それぞれの電源が1つしかないものと仮定して計算した場合に、それらの和がもとの電気回路の値と一致する、というものです。

また、この際、電圧源は電圧が掛かっていないものと見なすため、短絡状態とします。そして、電流源は電流が流れていないものと見なすため、開放状態とします。

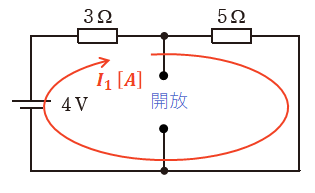
以上を踏まえて、まずは電圧源のほうから考えます。この場合、上記の通り電流源はないもの(開放状態)と見なしてください。すると、この問題の回路は以下の図のように表すことができるので、このときに3[Ω]の抵抗を流れる電流I₁は次のように計算できます。

続いて、電流源について考えます。この場合、電圧源はないもの(短絡状態)と見なしてください。すると、問題の回路は以下の図のように表すことができ、このときに3[Ω]の抵抗を流れる電流I₂を算出することができます。

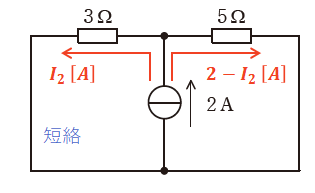
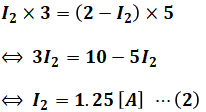
以上から、問題の図の直流回路において、3[Ω]の抵抗を流れる電流の値I[A]は、次のように求めることができます。ここでの注意点として、I₁とI₂は上図の通り流れる電流の向きが反対であるため、その合成であるIを求める際には、足し算ではなく差し引きによって求める必要があります。

よって、正解は(5)となります。