問 題
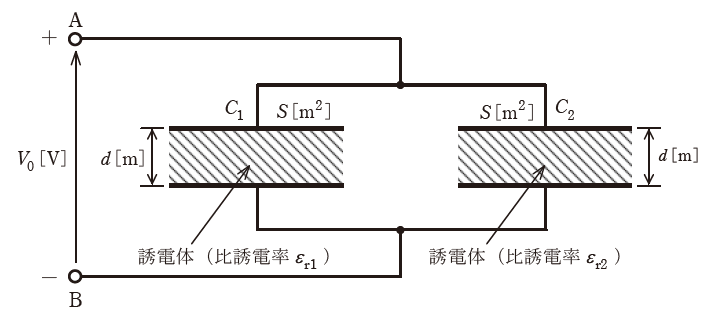
電極板面積と電極板間隔が共にS[m2]とd[m]で、一方は比誘電率がεr1の誘電体からなる平行平板コンデンサC1と、他方は比誘電率がεr2の誘電体からなる平行平板コンデンサC2がある。
今、これらを図のように並列に接続し、端子A、B間に直流電圧V0[V]を加えた。このとき、コンデンサC1の電極板間の電界の強さをE1[V/m]、電束密度をD1[C/m2]、また、コンデンサC2の電極板間の電界の強さをE2[V/m]、電束密度をD2[C/m2]とする。
両コンデンサの電界の強さE1[V/m]とE2[V/m]はそれぞれ( ア )であり、電束密度D1[C/m2]とD2[C/m2]はそれぞれ( イ )である。したがって、コンデンサC1に蓄えられる電荷をQ1[C]、コンデンサC2に蓄えられる電荷をQ2[C]とすると、それらはそれぞれ( ウ )となる。
ただし、電極板の厚さ及びコンデンサの端効果は、無視できるものとする。また、真空の誘電率をε0[F/m]とする。
上記の記述中の空白箇所(ア)~(ウ)に当てはまる式の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
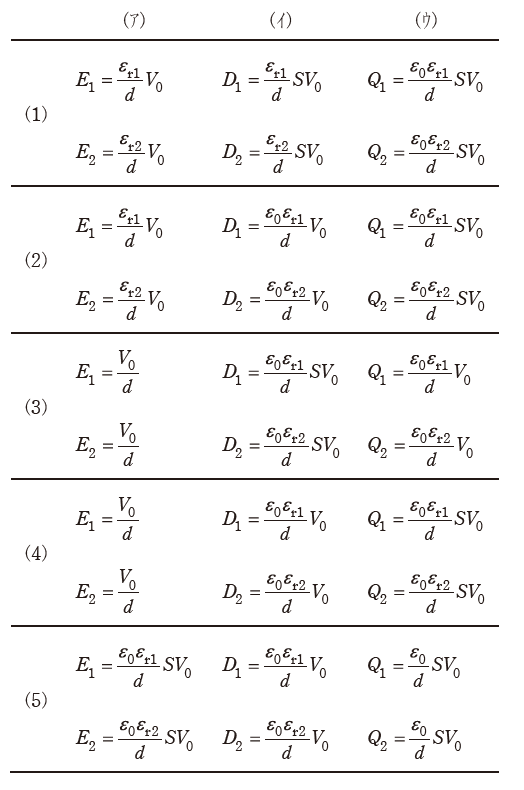
解 説
( ア )について、コンデンサC1とC2は並列接続なので、端子電圧はどちらもV0[V]です。よって、以下の(1)式に示す電界の強さの式から、電界の強さをE1、E2は次の(2)式のように表すことができます。(1)式は重要公式として押さえておいてください。
![]()
- V:電圧 [V]
- d:板間距離 [m]
- E:電界の強さ [V/m]
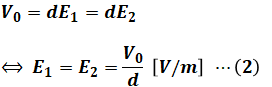
よって、( ア )には「![]() 」が入ります。
」が入ります。
( イ )に関して、電束密度Dというのは1[m2]あたりの電束の数で、その単位は問題文にもある通り[C/m2]です。これは、次の(3)式のように電界の強さEと誘電率εとの積で表すことができます。
![]()
- D:電束密度 [C/m2]
- E:電界の強さ [V/m]
- ε:誘電率 [F/m]
- ε0:真空の誘電率 [F/m]
- εr:比誘電率 (単位なし)
ここで、( イ )に入る選択肢を見ると、どこにもEが含まれていないため、(3)式をそのまま答えには当てはめられません。そこで、(2)式を(3)式に代入することで、次の(4)式のように( イ )に入る式を求めることができます。
![]()
よって、( イ )には「![]() 」が入ります。
」が入ります。
( ウ )について、電荷Q[C]は静電容量C[F]と電圧V[V]を使って以下の(5)式で表されます。
![]()
- Q:電荷 [C]
- C:静電容量 [F]
また、静電容量C[F]は問題文で与えられている各パラメータを使って(6)式の通り表すことができます。
![]()
- ε:誘電率 [F/m]
- ε0:真空の誘電率 [F/m]
- εr:比誘電率 (単位なし)
- S:板の面積 [m2]
- d:板間距離 [m]
よって、(5)式と(6)式から、電荷Qは次の(7)式のようになります。
![]()
よって、( ウ )には「![]() 」が入ります。
」が入ります。
以上から、正解は(4)となります。

コメント