問 題
30件分の使用電力量のデータ処理について、次の(a)及び(b)に答えよ。
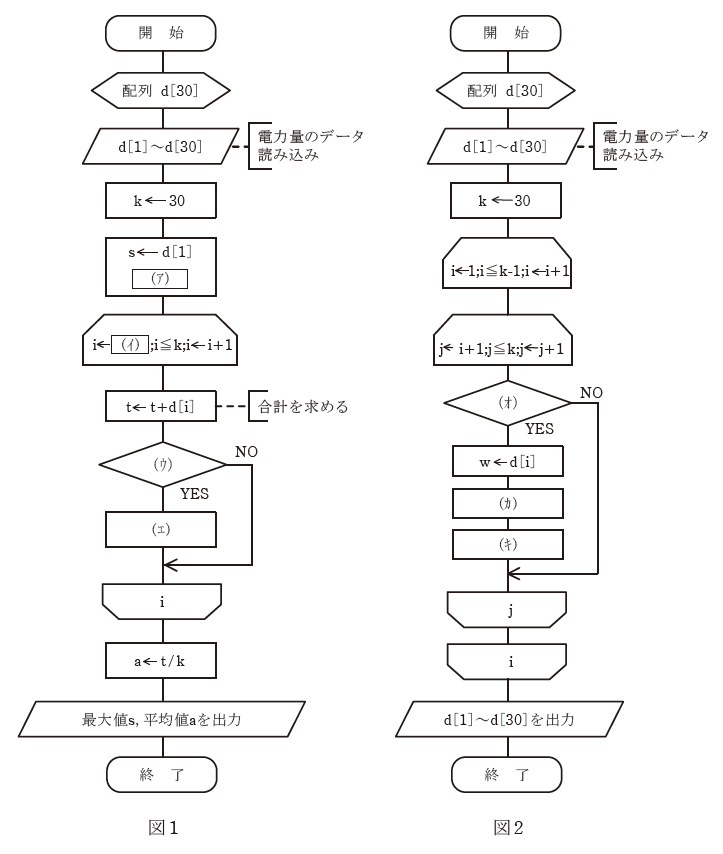
(a) 図1は、30件分の使用電力量の中から最大値と30件分の平均値を出力する一つのプログラムの流れ図を示す。図1中の(ア)～(エ)に当てはまる処理として、正しいものを組み合わせたのは次のうちどれか。
- (ア) (イ) (ウ) (エ)
- t←d[1] 0 d[i]＜s s←d[i]
- t←0 2 d[i]＞s s←d[i]
- t←d[1] 2 d[i]＜s d[i]←s
- t←d[1] 2 d[i]＞s s←d[i]
- t←0 0 d[i]＜s d[i]←s
(b) 図2は、30件の使用電力量を大きい順(降順)に並べ替える一つのプログラムの流れ図を示す。図2中の(オ)～(キ)に当てはまる処理として、正しいものを組み合わせたのは次のうちどれか。ただし、wは一時的な退避用の変数と考えよ。
- (オ) (カ) (キ)
- d[i]＜d[j] d[j]←d[i] d[j]←w
- d[i]＜d[j] d[i]←d[j] d[j]←w
- d[i]＜d[j] d[j]←d[i] d[i]←w
- d[i]＞d[j] d[i]←d[j] d[j]←w
- d[i]＞d[j] d[j]←d[i] d[i]←w
解 説
(a)
まず、解説のときに参照しやすいように、図1の各段に以下のような番号を付けます。
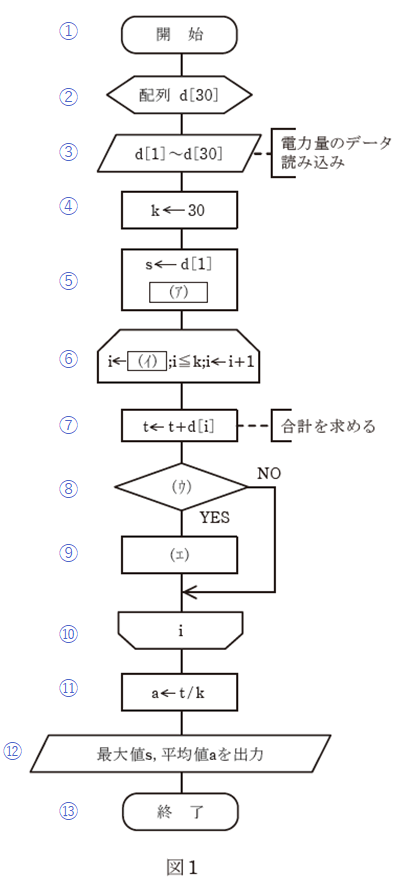
上図において、②で30個の配列を用意し、③ではそこに各電力量のデータを読み込ませています。そして、④でデータの全数が30であることを定義しています。
続く⑤では、1つ目のデータであるd[1]の値をsに代入していますが、この「s」というのは、⑫を見ると「最大値」を表す記号であることがわかります。つまり、1つ目のデータを扱っている時点では、d[1]が現時点の最大値であるということです。
ここで、( ア )の選択肢を見ると、全ての選択肢にtが含まれています。この「t」について、⑦を見ると『t←t＋d[i] 合計を求める』とあることから、tは「現時点での合計」であると考えることができます。
また、⑪には『a←t/k』とあり、kはデータの全数(④参照)で、aは平均値(⑫参照)なので、⑪時点のtは30個分のデータの合計値を表していることがわかります。つまり、⑥～⑩のループを繰り返すことによって30個分のデータの合計値を1つずつ蓄積し、最終的に⑪で全データの平均値を算出しています。
ただし、ループに入る前の⑤の時点ではまだ1つのデータ(d[1])しか扱っていません。そのため、この時点での合計値tは、d[1]の値そのものです。よって、( ア )には「t←d[1]」を入れるのが適切です。
次に、⑥の( イ )には選択肢から「0」または「2」が入るようです。どちらが正しいのかは⑥だけを見ているとわかりづらいですが、⑥と⑦を合わせることで考えやすくなると思います。
⑦には『t←t＋d[i]』とあるので、「i」は③の電力量のデータ『d[1]～d[30]』のうち「1～30」の各番号に相当することがわかります。つまり、iには1～30の数値が入るはずなので、0となることはなく、⑥で『i←0』としてしまうのは不適当であると判断できます。つまり、( イ )は「2」となります。
そこで、( イ )に「2」を入れた場合にどうなるかというと、⑥に書かれている3つの式は次のような意味を持ちます。
- 左側『i←2』：初めてループに入ったときだけに適用される式で、iの値を2とします。
- 中央『i≦k』：ループを繰り返すための条件を設定する式で、iがk(＝30)以下である場合にループが継続されることになります。
- 右側『i←i＋1』：ループが行われたあとに実行される処理で、今までのiの値に1が足されます。
以上から、最初に⑥に到達したときには「i＝2」となり、⑥～⑩でd[1]とd[2]の合計と最大値を求め、その後「i＝3」とします。そして、「i＝3」でも同様にループ⑥～⑩によりd[1]～d[3]の合計と最大値を求め、「i＝4」となります。
これを「i＝30」まで繰り返し実行し、⑥にて「i＝31」になった時点で⑦～⑩を飛ばして⑪へと進みます。そして⑪で30個分のデータの平均値を求め、⑫で最大値sと平均値aを出力します。
ここまでの解説で、全体の流れに加えて( ア )と( イ )の答えがわかったので、以下では残る( ウ )と( エ )の答えを確認していきます。
( ウ )と( エ )の選択肢を見ると、⑧と⑨で行う処理の意味合いは次のようになると考えることができます。
- ⑧：i番目のデータd[i]と現時点の最大値sを比較する。
- ⑨：⑧のd[i]がsよりも大きいなら、その値(d[i])を新しい最大値sとする。
よって、⑧ではd[i]とsを比較して、d[i]のほうが大きい場合に⑨で最大値の更新を行うので、( ウ )には「d[i]＞s」が、( エ )には「s←d[i]」が入ることがわかります。
以上から、( ア )は「t←d[1]」、( イ )は「2」、( ウ )は「d[i]＞s」、( エ )は「s←d[i]」となるので、正解は(4)です。
(b)
設問(b)は、数値の大きい順に並べるフローチャートに関する出題です。これは頻出テーマなので、特に解法をしっかり理解しておきたい問題といえます。
まずは設問(a)と同様、図2の各段に以下のような番号を付け、その番号を使いながら解説していきます。
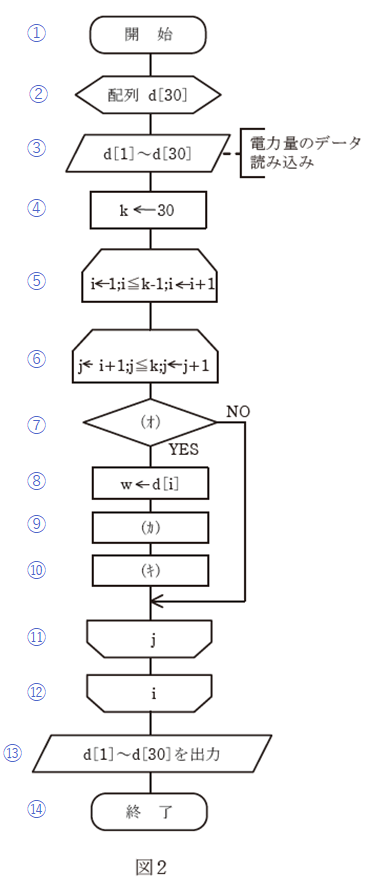
フローチャートを上から見ていくと、①で「開始」して、②で配列が全部で30個であることが示され、③でその30個のデータを読み込みます。そして、④ではデータの全数が30であることが示されています。
このあとの⑤では3つの式が書かれていますが、その解釈は設問(a)のときと同じく、次のようになります。
- 左側『i←1』：初めてループに入ったときだけに適用される式で、iの値を1とします。
- 中央『i≦k－1』：ループを繰り返すための条件を設定する式で、iがk－1(＝29)以下である場合にループが継続されることになります。
- 右側『i←i＋1』：ループが行われたあとに実行される処理で、今までのiの値に1が足されます。
そして、⑥でも⑤と同じような3つの式が書かれています。左側には「j←i+1」とあるので、iとjは連続する2つ値(jのほうが1だけ大きい)となります。
次に、⑦のひし形で表される「判断」で、2つの数値の大小を比較します。このフローチャートの目的は数値を大きい順に並べることなので、2つの数値を比べてみた結果、正しい順序ならスルー、間違った順序なら数値を入れ替えるという操作がここで行われます。
比較条件は( オ )となっていて、選択肢を見るとd[i]とd[j]を比べることがわかります。上記の通り、jはiよりも1だけ大きい値なので、d[i]とd[j]の関係は、たとえば「1番目と2番目」や「4番目と5番目」といった関係となります。
最終的に大きい順に並べたいので、d[i]がd[j]より小さいと良くないので入れ替えが必要で、d[i]がd[j]より大きいなら理想的なので何も変える必要はありません。
ここでフローチャートを見ると、⑦の直下にある⑧～⑩の部分で数値の入れ替えを行っていると判断できるので、d[i]がd[j]より小さいならYESを進んで⑧～⑩で入れ替え処理をし、d[i]がd[j]より大きいならNO側からそのまま次に進めばよいことがわかります。
よって、( オ )では「d[i]がd[j]より小さいか？」という質問をすればよいことになるので、( オ )には「d[i]＜d[j]」が入ります。
続いて、( カ )と( キ )を含んだ⑧～⑩の部分を見ていきます。
ここでは「処理」が3つ連続でありますが、やりたいことは上記の通り、d[i]とd[j]の値を交換することです。2つの値を直接入れ替えることはできないので、wを間にはさむことで数値の入れ替えをしています。
この流れ(フローチャートの⑧～⑩)は、次の通りです。
- まず、⑧でd[i]の値をmの値に代入します。これにより、d[i]の値をwという場所に仮置きすることができます。
- 次に、⑨でd[j]の値をd[i]の値に代入します。これによりd[i]の元の値は消えてしまいますが、wに仮置きしておいたので大丈夫です。
- 最後に、⑩でwの値をd[j]の値に代入します。wの値はもともとd[i]だった値です。
- 以上で、d[i]とd[j]の値が入れ替わります。
上記の流れから、( カ )には「d[i]←d[j]」が、( キ )には「d[j]←w」が入ることがわかります。
もし( カ )で「d[j]←d[i]」としてしまうと、まだd[j]の元の値をどこにも保存していない状態で別の数値を上書きすることになるので、d[j]の元の値が消えてしまいます。
また、( キ )に「d[i]←w」を入れた場合は、⑧の「w←d[i]」を逆にしただけなので、d[i]は元の値がそのまま戻ってくることになり、d[j]との交換になりません。
以上から、( オ )は「d[i]＜d[j]」、( カ )は「d[i]←d[j]」、( キ )は「d[j]←w」となるので、正解は(2)です。
コメント