電験三種 R4年度下期 機械 問17 問題と解説

　問 題　　　　　

どの方向にも光度が等しい均等放射の点光源がある。この点光源の全光束は3000lmである。この点光源を図のように配置した。水平面から点光源までの高さは2mであり、点光源の直下の点AとBとの距離は1.5mである。次の(a)及び(b)の問に答えよ。

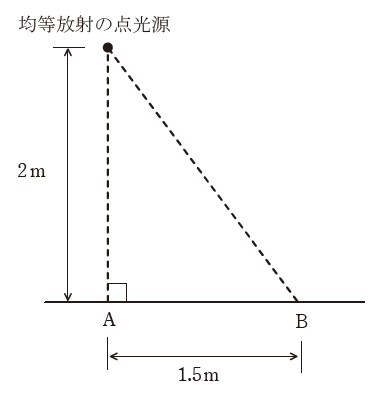
(a)　この点光源の平均光度[cd]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 191
2. 239
3. 318
4. 477
5. 955

(b)　水平面B点における水平面照度の値[lx]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 10
2. 24
3. 31
4. 61
5. 122

 

 

 

 

 

　解 説　　　　

(a)

設問(a)では点光源の平均光度が問われていますが、光度I[cd]は光束F[lm]を立体角ω[sr]で割ったものです。また、ωは面積Sを半径rの2乗で割ったものとなりますが、今回のように点光源であれば、その光は球の形で広がり、その面積は球の表面積4πr²となります。

よって、光度I[cd]を求める計算式は以下のようになります。

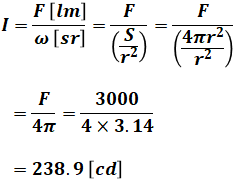
以上から、正解は(2)となります。

(b)

水平面照度Eと光度I_θの関係式は以下の(1)式で表すことができます。

• E：水平面照度 [lx]
• I_θ：光度 [cd]
• r：点光源と観測点との距離 [m]
• θ：点光源の直下方向と観測点とのなす角

光度I_θは、設問(a)より239[cd]となります。また、距離rと角θは問題の図より、次のように計算できます。

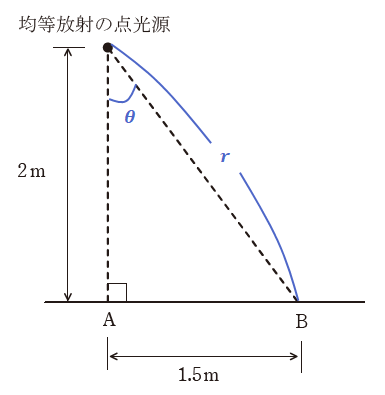
よって、(2)式と(3)式を(1)式に代入すれば、水平面照度Eを計算することができます。

以上から、正解は(3)となります。