問 題
図は、抵抗、インダクタンス、キャパシタンスで構成されたRLC回路である。次の(a)及び(b)の問に答えよ。
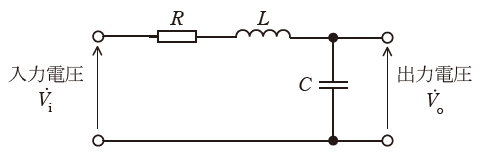
(a) 図において、入力電圧
に対する出力電圧
の伝達関数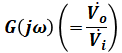
を求め、正しいものを次の(1)～(5)のうちから一つ選べ。
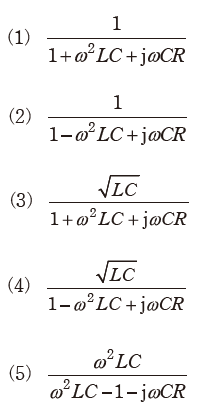
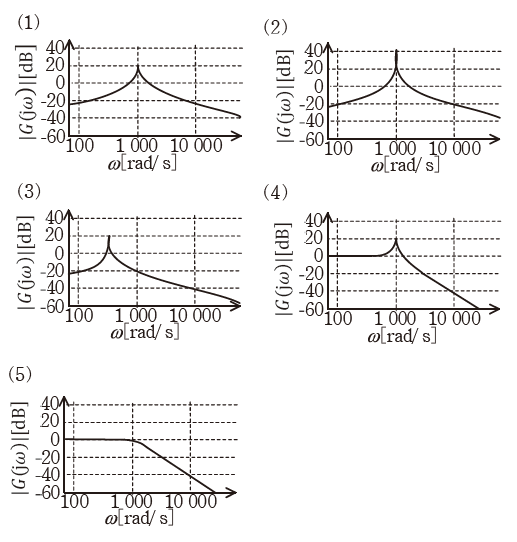
(b) 図において、R＝1Ω、L＝0.01H、C＝100μFとした場合、(a)で求めた伝達関数を表すボード線図(ゲイン特性図)として、最も近いものを次の(1)～(5)のうちから一つ選べ。
解 説
(a)
問題の図はRLC直列回路であるので、以下のような等価回路で表すことができます。
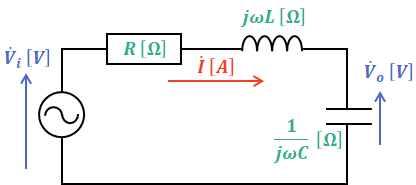
上図より、入力電圧と出力電圧はそれぞれ以下の(1)式、(2)式のようになります。
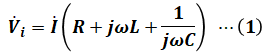
よって、伝達関数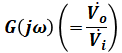は次のように計算することができます。
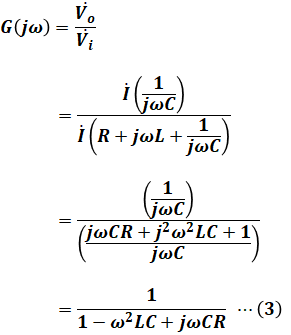
以上から、正解は(2)となります。
(b)
設問(b)ではボード線図のグラフが問われていますが、選択問題なので、各選択肢の中で違いの出そうなω＝0、100、1000、10000あたりに注目して比較をすればよいと思います。
具体的には、まずは設問(a)の(3)式にR、L、C、ωの値を代入し、丨G(jω)丨を求めます。
ここで注意点として、各選択肢の縦軸は丨G(jω)丨と書かれていますが、その単位が[dB]と明記されています。この単位はゲイン特性を表していて、そのゲイン特性g[dB]は次の式で定義されます。これは重要事項として覚えておくべき公式です。
よって、解法の方針としては、(3)式にω＝0を代入して丨G(jω)丨を求めたら、次に(4)式を使ってgを計算し、それに見合う選択肢を絞ります。続いて、ω＝100を代入して同じことをし、さらにω＝1000やω＝1000でも繰り返せば、いずれは選択肢が一つに限定されると予想されます。
そこで、まずはω＝0のとき、(3)式より丨G(jω)丨は次のようになります。
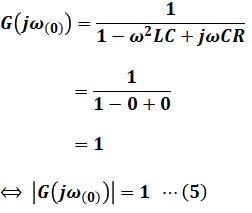
よって、このときのゲイン特性g[dB]は(4)式を使うと次のように計算できます。
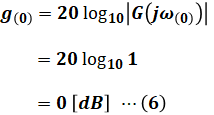
この時点でω＝0のときにg＝0[dB]となるものを探すと、選択肢は(4)と(5)に絞られます。
続いて、ω＝100だと選択肢(4)と(5)で同じゲイン特性g[dB]になりそうなので、違いの出そうなω＝1000について先ほどと同様の計算を行います。
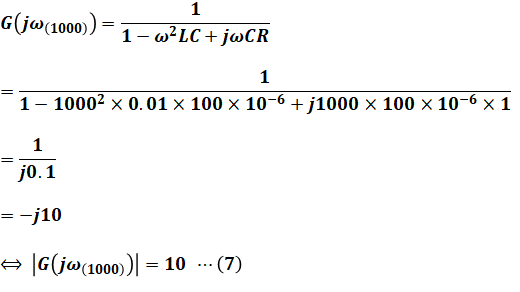
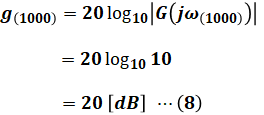
よって、選択肢は(4)と(5)の中では、選択肢(4)だけが(8)式に当てはまるため、正解は(4)だと判断できます。
当初の予定ではω＝100やω＝10000についても試してみるつもりでしたが、すでに正解の選択肢が一つに絞られたので、ここでは割愛します。試験中に時間に余裕があれば、検算のつもりで計算してもよいかもしれません。
以上から、正解は選択肢(4)となります。
コメント