問 題
図のように配電用変圧器二次側の単相3線式低圧配電線路に負荷A及び負荷Bが接続されている場合について、次の(a)及び(b)の問に答えよ。
ただし、変圧器は、励磁電流、内部電圧降下及び内部損失などを無視できる理想変圧器で、一次電圧は6600V、二次電圧は110/220Vで一定であるものとする。
また、低圧配電線路及び中性線の電線1線当たりの抵抗は0.06Ω、負荷A及び負荷Bは純抵抗負荷とし、これら以外のインピーダンスは考慮しないものとする。
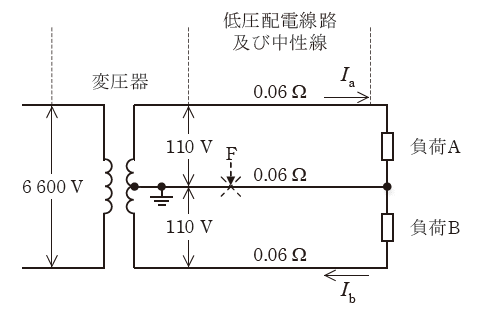
(a) 変圧器の電流を測定したところ、一次電流が5A、二次電流IaとIbの比が2:3であった。二次側低圧配電線路及び中性線における損失の合計値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 2.59
- 2.81
- 3.02
- 5.83
- 8.21
(b) 低圧配電線路の中性線が点Fで断線した場合に負荷Aにかかる電圧の値[V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 88
- 106
- 123
- 127
- 138
解 説
(a)
まずは、問題の図に電流、電圧、抵抗の記号を描き込むと、次のように図示できます。
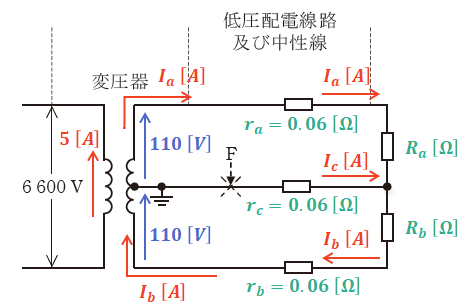
ここで、上図変圧器のところに注目すると、一次電圧の電流が5[A]で、電圧が6600[V]で、これらの積が一次側の電力になります。そして、変圧器では一次側と二次側の電力は不変なので、以下の等式が成り立ちます。
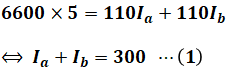
一方で、設問(a)の問題文より「Ia:Ib=2:3」なので、次の等式が成り立ちます。
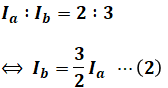
よって、(1)式と(2)式の連立方程式を解くと、Ia、Ibの値を算出することができます。
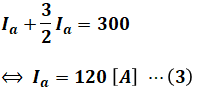
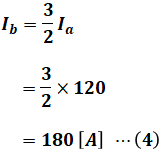
以上のことを上図にまとめると、下図のように描き換えることができます。なお、中性線を流れる電流Icは、IbとIaの差し引きから算出しています。
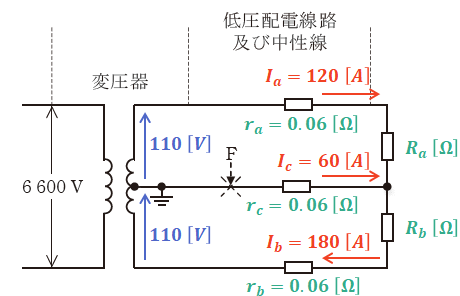
よって、上図を見ると二次側低圧配電線路及び中性線のそれぞれの抵抗と電流の値がわかるので、これらでの損失の合計値Ploss[kW]は次のように計算することができます。
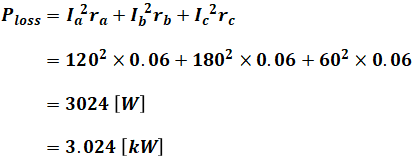
以上から、正解は(3)となります。
(b)
設問(b)では点Fで断線しているため、問題の図は次のような状態となっています。
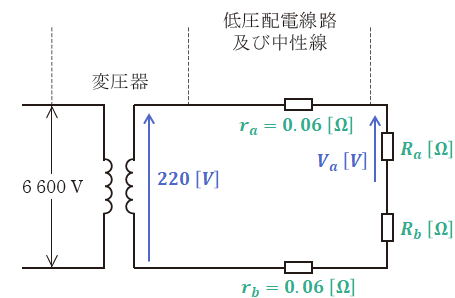
上図において、問われているのは負荷Aにかかる電圧の値Va[V]です。そして、これは上図のRaとRbの値がわかれば、比の計算から求めることができます。そのため、当面の目標は、RaとRbの値を計算することとなります。
ここで、設問(a)と設問(b)では同じ抵抗を用いているため、抵抗値RaやRbはどちらの設問でも同じ値となります。よって、設問(a)で使った図(断線前の条件)についてもう一度考えます。
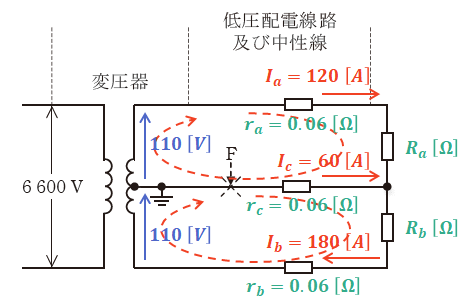
上図の点線赤矢印で示した2つの回路について、それぞれキルヒホッフの第二法則(電圧則)を用いると、以下の等式が成り立ち、RaとRbを算出することができます。
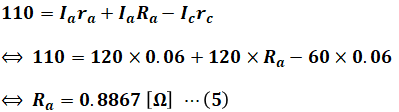
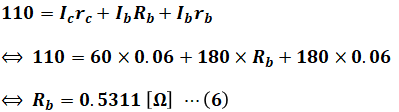
(5)式と(6)式の結果を設問(b)の条件の図に書き加えると、次のように表すことができます。
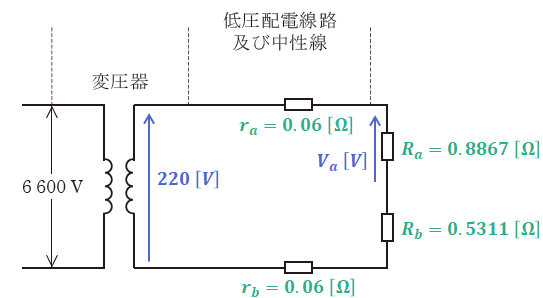
よって、抵抗4つ分を合わせた分の端子電圧が220[V]なので、抵抗Raの端子電圧は次のように計算できます。
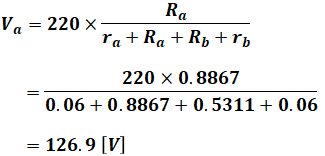
以上から、正解は(4)となります。

コメント