電験三種 R4年度下期 電力 問16 問題と解説

　問 題　　　　　

電線1線の抵抗が6Ω、誘導性リアクタンスが4Ωである三相3線式送電線について、次の(a)及び(b)の問に答えよ。

(a)　受電端電圧を60kV、送電線での電圧降下率を受電端電圧基準で10%に保つものとする。この受電端に、力率80%(遅れ)の負荷を接続する。

この場合、受電可能な三相皮相電力の値[MV・A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 28.9
2. 42.9
3. 50.0
4. 60.5
5. 86.6

(b)　受電端に接続する負荷の条件を、遅れ力率60%、三相皮相電力65MV・Aに変更することになった。この場合でも、受電端電圧を60kV、送電線での電圧降下率を受電端電圧基準で10%に保ちたい。

受電端に設置された調相設備から系統に供給すべき無効電力の値[Mvar]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 12.0
2. 20.5
3. 27.0
4. 31.5
5. 47.1

 

 

 

 

 

　解 説　　　　

(a)

問われているのは受電可能な三相皮相電力の値S[MV・A]です。そのため、まずはこれを式で表すと、次のように書くことができます。

• S：皮相電力 [V・A]
• V_r：受電端電圧 [V]
• I：電流 [A]

上式において、V_rはすでに60[kV]とわかっているので、このあとIを求めて(1)式に代入することでSを算出するのが、解法の方針となります。

ここで、(a)の問題文に「送電線での電圧降下率を受電端電圧基準で10%に保つ」とあるので、電圧降下率εを式で表し、これが最大の10[%]になるときの電圧降下V_dについて考えます。

• ε：電圧降下率 [%]
• V_d：電圧降下 [V]
• V_r：受電端電圧 [V]

一方で、三相3線式送電線における電圧降下の式は、以下のように表すことができます。これは重要公式としてそのまま覚えておきたい知識ですが、もし導出方法を知りたい場合は三相3線式送電線の電圧降下のページを参照してください。

• V_d：電圧降下 [V]
• V_s：送電端電圧 [V]
• V_r：受電端電圧 [V]
• I：線電流 [A]
• R：抵抗(電線1条あたり) [Ω]
• X：リアクタンス(電線1条あたり) [Ω]
• cosθ：負荷の力率

上式において、(2)式と問題文で与えられた各数値から、V_d、R、X、cosθはわかっています。そのため、(3)式をIについて解けば、Iを求めることができます。

よって、(4)式を(1)式に代入すれば、求めたい皮相電力Sを算出することができます。

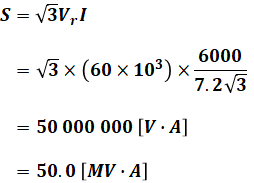
以上から、正解は選択肢(3)となります。

(b)

設問(b)では、調相設備から系統に対して無効電力を供給することで、力率改善を行っています。この状況を図示すると、次のように表すことができます。

      

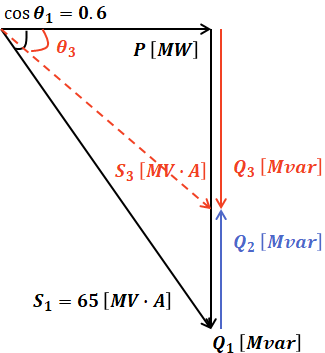
上図において、Q₂が力率改善のために供給する無効電力に相当し、この値が最終的に求めたい答えです。また、Q₁はもともとの負荷の無効電力、Q₃は力率改善後の無効電力となります。

Q₂を直接求めるのは難しそうなので、まずはQ₁とQ₃を求め、その差し引きでQ₂を算出するというのが現実的な解法になると思います。

そのため、まずは上図から読み取れる情報として、皮相電力S₁がわかっているので、有効電力Pと無効電力Q₁はすぐに計算することができます。

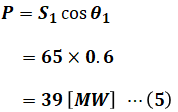
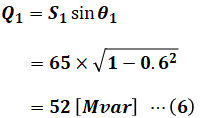
これによりQ₁がわかったので、次はQ₃を導出することを目指します。

Q₃は力率改善後の無効電力なので、上図赤色で示した部分について考えると、PとQ₃はそれぞれ次の式で表すことができます。なお、Pについては、力率改善前後で数値が変わることはありません。

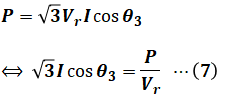
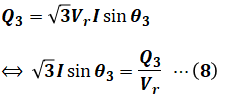
ここで、上記の形は設問(a)の(3)式でも使った電圧降下の式に似ているため、改めてその式を持ってきます。

なお、設問(b)でも設問(a)と同様に「受電端電圧を60kV、送電線での電圧降下率を受電端電圧基準で10%に保ちたい」とあるので、設問(a)の(2)式より、V_d＝6000[V]です。

よって、(9)式に(7)式と(8)式を代入して、Q₃について解けば、Q₃の値を計算することができます。ここで、問題文よりR＝6[Ω]、Q＝4[Ω]、V_r＝60×10³[V]で、(5)式よりP＝39×10⁶[W]です。

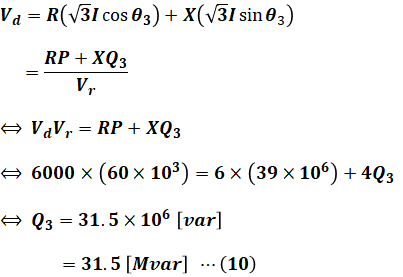
(6)式と(10)式により、Q₁とQ₃の値がわかったので、問われているQ₂の値は次の通りです。

以上から、正解は(2)となります。