電験三種 R4年度下期 電力 問15 問題と解説

　問 題　　　　　

復水器での冷却に海水を使用する汽力発電所が出力600MWで運転しており、復水器冷却水量が24m³/s、冷却水の温度上昇が7℃であるとき、次の(a)及び(b)の問に答えよ。

ただし、海水の比熱を4.02kJ/(kg・K)、密度を1.02×10³kg/m³、発電機効率を98%とする。

(a)　復水器で海水へ放出される熱量の値[kJ/s]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 4.25×10⁴
2. 1.71×10⁵
3. 6.62×10⁵
4. 6.89×10⁵
5. 8.61×10⁵

(b)　タービン室効率の値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、条件を示していない損失は無視できるものとする。

1. 41.5
2. 46.5
3. 47.0
4. 47.5
5. 48.0

 

 

 

 

 

　解 説　　　　

(a)

復水器で海水へ放出される熱量の値Q[kJ/s]は、次の式で求められます。これは公式として押さえておきたいところですが、仮に覚えていなくても、単位に注目すればわかりやすいと思います。

なお、下式の比熱の単位に出てくる[K](ケルビン)は[℃]に置き換えられる点がポイントです。Kは絶対温度、℃は摂氏として使われますが、「温度差」として用いる限りは両者を区別する必要はありません。

• Q：熱量 [kJ/s]
• c：比熱 [kJ/kg・K]
• m：質量流量 [kg/s]
• Δθ：上昇温度 [K]

ここで、mは復水器冷却水の質量流量[kg/s]ですが、これは以下に示すように密度[kg/m³]と流量[m³/s]との積で求めることができます。

• ρ：密度 [kg/m³]
• V：流量 [m³/s]

(2)式を(1)式に代入し、問題文で与えられた各数値を代入して次のように計算を進めると、求めたいQの値を算出することができます。

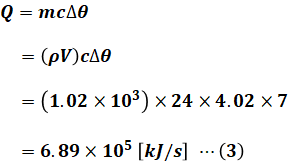
よって、正解は選択肢(4)となります。

(b)

問題文と設問(a)の計算結果からわかっていることをまとめると、下図のように表すことができます。

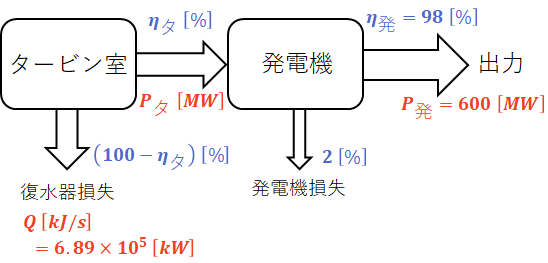
• η：(タービン室または発電機の)効率 [%]
• P：(タービン室または発電機の)出力 [MW]

上図より、発電機出力P_発＝600[MW]であり、発電機効率η_発＝98[%]なので、タービン室出力P_タは次のように計算できます。

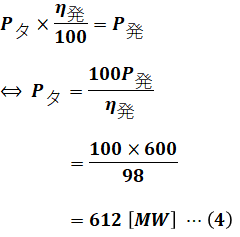
よって、上図のタービン室に注目すると、(3)式よりQの値はわかっていて、(4)式よりP_タもわかりました。そのため、以下の比の計算によって、タービン室効率η_タを算出することができます。

なお、設問(a)で求めたQの単位は[kJ/s]でしたが、[J/s]＝[W]なので、[kJ/s]＝[kW]となります。さらに、P_タの単位[MW]と合わせるため、Q＝6.89×10⁵[kW]＝6.89×10²[MW]＝689[MW]としてから比の計算を行います。

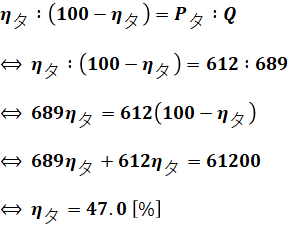
以上から、正解は(3)となります。