問 題
交流三相3線式1回線の送電線路があり、受電端に遅れ力率角θ[rad]の負荷が接続されている。送電端の線間電圧をVs[V]、受電端の線間電圧をVr[V]、その間の相差角はδ[rad]である。
受電端の負荷に供給されている三相有効電力[W]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、送電端と受電端の間における電線1線当たりの誘導性リアクタンスはX[Ω]とし、線路の抵抗、静電容量は無視するものとする。
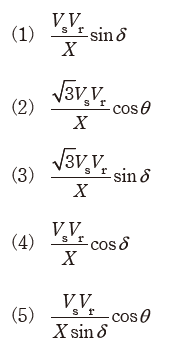
正解 (1)
解 説
本問では、交流三相3線式1回線の、受電端の負荷に供給されている三相有効電力[W]が問われています。
ここで、三相3線式送電線の送電電力(有効電力)P[W]は以下の式で表されます。下式を使う問題がたびたび出題されるので、ぜひ公式として押さえておいてください。今回はこれを覚えておくだけで解けるので、易しい設問だといえます。
![]()
- P:三相3線式送電線の送電電力(有効電力) [W]
- Vs:送電端の線間電圧 [V] (supplyの”s”)
- Vr:受電端の線間電圧 [V] (receiveの”r”)
- X:線路リアクタンス [Ω]
- δ:Vs-Vr間の相差角
よって、この公式を知っていれば正解は(1)だとすぐにわかります。
上記の公式は、回路図とベクトル図を描いて計算によって導出することもできますが、導出過程を問う問題はほとんど見られません。むしろ、この公式を用いて計算を進める問題のほうが頻出です。そのため、上式をそのまま覚えてしまうことをお勧めします。

コメント