電験三種 R4年度下期 電力 問6 問題と解説

　問 題　　　　　

定格値が一次電圧66kV、二次電圧6.6kV、容量30MV・Aの三相変圧器がある。一次側に換算した漏れリアクタンスの値が14.5Ωのとき、百分率リアクタンスの値[%]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 3.3
2. 5.8
3. 10.0
4. 17.2
5. 30.0

 

 

 

 

 

　解 説　　　　

本問では百分率リアクタンス[%]が問われていますが、これは百分率インピーダンス(%Z)[%]と同じようなものです。正確には、抵抗R[Ω]とリアクタンスX[Ω]の合力をインピーダンスZ[Ω]といいますが、今回はリアクタンスしか登場しないので、リアクタンスX＝インピーダンスZと考えて大丈夫です。

ここで、百分率インピーダンス(%Z)は下式で表されます。この式は重要公式として押さえておくべき式です。

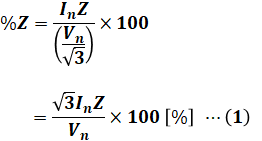
問題文で与えられた各数値を(1)式に代入すれば%Zを計算することができそうですが、現状では定格電流I_nが未知数です。一方で容量P_nはわかっているので、まずは次のようにI_nとP_nの関係式を立てます。

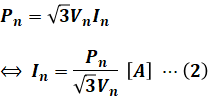
そして、(2)式を(1)式に代入しつつ、問題文で与えられた容量P_n＝30[MV・A]や、定格一次電圧V_n＝66[kV]、Z＝14.5[Ω]を使えば、%Z[%]の値を計算することができます。

なお、なぜ二次電圧ではなく一次電圧の数値を使うかというと、問題文に「一次側に換算した漏れリアクタンスの値が14.5Ω」という記述があるためです。与えられたこの数値を使うために、電圧についても一次側の数値にそろえる必要があります。

以上を踏まえると、%Z[%]は次のように計算することができます。

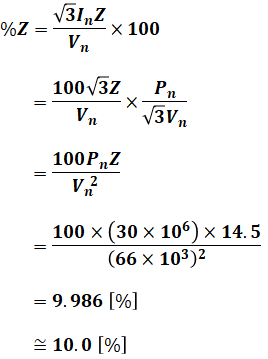
よって、正解は(3)となります。