問 題
最大目盛50A、内部抵抗0.8×10-3Ωの直流電流計A1と最大目盛100A、内部抵抗0.32×10-3Ωの直流電流計A2の二つの直流電流計がある。次の(a)及び(b)の問に答えよ。
ただし、二つの直流電流計は直読式指示電気計器であるとし、固有誤差はないものとする。
(a) 二つの直流電流計を並列に接続して使用したとき、測定できる電流の最大の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 40
- 50
- 100
- 132
- 140
(b) 小問(a)での接続を基にして、直流電流150Aの電流を測定するために、二つの直流電流計の指示を最大目盛にして測定したい。そのためには、直流電流計A2に抵抗R[Ω]を直列に接続することで、各直流電流計の指示を最大目盛にして測定することができる。
抵抗Rの値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 3.2×10-5
- 5.6×10-5
- 8×10-5
- 11.2×10-5
- 13.6×10-5
解 説
(a)
直流電流計A1は最大目盛50[A]、内部抵抗0.8×10-3[Ω]なので、電流計に掛けることのできる最大電圧V1maxは次のように計算できます。
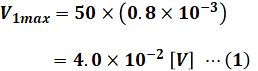
同様に、直流電流計A2は最大目盛100[A]、内部抵抗0.32×10-3[Ω]なので、電流計に掛けることのできる最大電圧V2maxは次のように計算できます。
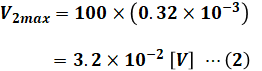
今回はこれら2つを並列に並べるので、2つの電流計の端子間電圧は等しいはずです。そのため、上で求めた2つの計算結果のうち小さいほうの3.2×10-2[V]が、この並列回路の最大許容電圧となります。
これらの情報をまとめると、以下のような図で表すことができます。
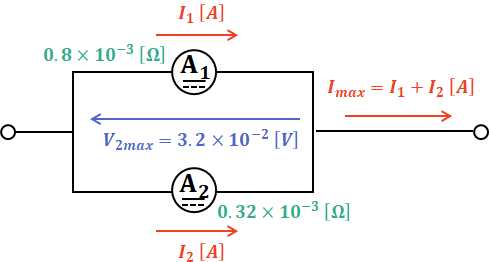
よって、測定できる電流の最大値Imaxは次のように計算することができます。

以上から、正解は(5)です。
(b)
(b)の問題文の最初に「直流電流150Aの電流を測定するために、二つの直流電流計の指示を最大目盛にして測定したい」と書かれています。これは重要なヒントなので、見落とさないようにしてください。
(a)での結果も踏まえると、要するに、直流電流計A1には最大電圧の4.0×10-2[V]を掛けて50[A]とし、直流電流計A2には最大電圧の3.2×10-2[V]を掛けて100[A]とすることで、合計150[A]の電圧を測定したい…という話です。
イメージ図を描くと、次のような感じです。
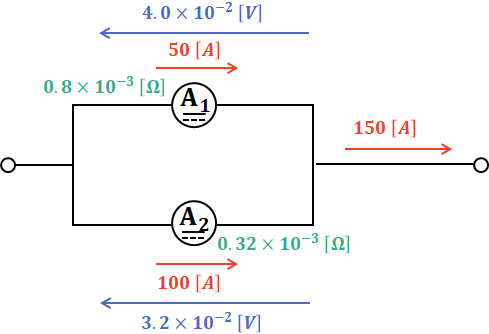
ただし、実際には上図のようにはなりません。(a)でも考えた通り、並列に並んだ電流計に掛かる電圧は必ず一致しているはずなので、上図のように電圧が異なっているのはおかしいです。
この矛盾を解消するために必要なのが、(b)の問題文の2文目以降に出てくる「抵抗R」です。この抵抗を、より内部抵抗の小さい直流電流計A2に直列に接続することで、下図のように2つの電流計ともを最大に生かすことができるようになります。
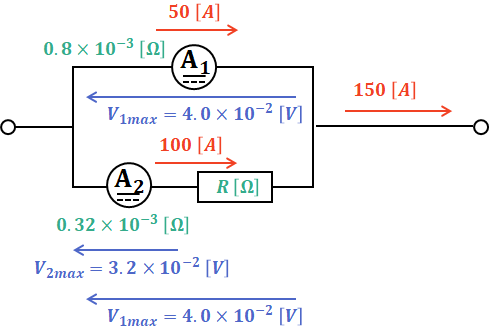
求めたいのは抵抗R[Ω]の値なので、上図より、抵抗Rの端子間電圧はV1maxからV2maxを引いた分となることがわかります。よって、R[Ω]は以下のような計算によって算出することができます。
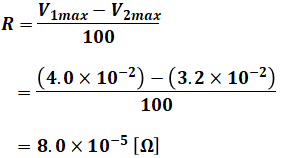
以上から、正解は(3)となります。

コメント