問 題
電圧E[V]の直流電源と静電容量C[F]の二つのコンデンサを接続した図1、図2のような二つの回路に関して、誤っているものを次の(1)~(5)のうちから一つ選べ。
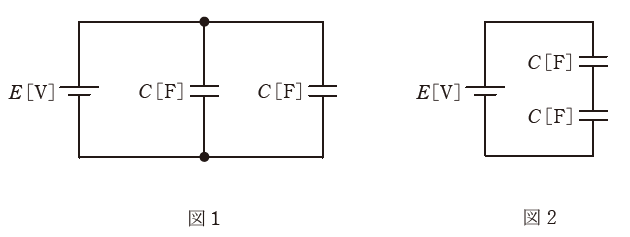
- 図1の回路のコンデンサの合成静電容量は、図2の回路の4倍である。
- コンデンサ全体に蓄えられる電界のエネルギーは、図1の回路の方が図2の回路より大きい。
- 図2の回路に、さらに静電容量C[F]のコンデンサを直列に二つ追加して、四つのコンデンサが直列になるようにすると、コンデンサ全体に蓄えられる電界のエネルギーが図1と等しくなる。
- 図2の回路の電源電圧を2倍にすると、コンデンサ全体に蓄えられる電界のエネルギーが図1の回路と等しくなる。
- 図1のコンデンサ一つ当たりに蓄えられる電荷は、図2のコンデンサ一つ当たりに蓄えられる電荷の2倍である。
解 説
まず、静電容量の合成について整理します。コンデンサが並列接続のときは、合成静電容量は各静電容量の和で表されます。コンデンサが直列接続のときは、合成静電容量の逆数は各静電容量の逆数の和で表されます。つまり、抵抗の合成に比べてちょうどの反対となります。
よって、問題の図1と図2の合成静電容量をそれぞれC1、C2とすると、次のように表すことができます。
![]()
![]()
以上を踏まえて、各選択肢の内容を確認していきます。
選択肢(1)で、上記の(1)式と(2)式より、C1は2C[F]、C2はC/2[F]なので、C1はC2の4倍となります。よって、これは正しい記述です。
選択肢(2)で、図1と図2の電界のエネルギーW1、W2は、(1)式や(2)式を使うと次のように計算できます。
![]()
![]()
よって、W1はW2よりも大きいので、これも正しい記述です。
選択肢(3)で、図2の回路にコンデンサをさらに2つ直列に追加した場合、合計で4つが直列に並ぶことになります。そのときのコンデンサ全体の合成静電容量C2(4)と電界のエネルギーW2(4)は、それぞれ次のように表すことができます。
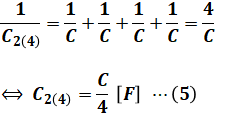
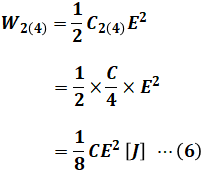
よって、(3)式と(6)式を比べると、W1とW2(4)は一致していないため、選択肢(3)の記述が誤りであると判断することができます。
選択肢(4)で、図2の回路の電源電圧を2倍にすると、そのときの電界のエネルギーW2(2E)は(4)式を利用すると次のように表されます。
![]()
よって、(3)式と(7)式を比べると、W1とW2(2E)は一致するため、これは正しい記述です。
選択肢(5)で、図1と図2のそれぞれで、コンデンサ1つあたりに蓄えられる電荷をQ1、Q2とすると、次のように計算することができます。
![]()
![]()
よって、Q1はQ2の2倍なので、これも正しい記述です。
以上から、正解は(3)となります。

コメント