電験三種 R4年度下期 理論 問4 問題と解説

　問 題　　　　　

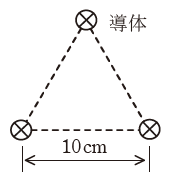
図のように、無限に長い3本の直線状導体が真空中に10cmの間隔で正三角形の頂点の位置に置かれている。3本の導体にそれぞれ7Aの直流電流を同一方向に流したとき、各導体1m当たりに働く力の大きさF₀の値[N/m]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、無限に長い2本の直線状導体をr[m]離して平行に置き、2本の導体にそれぞれI[A]の直流電流を同一方向に流した場合、各導体1m当たりに働く力の大きさFの値[N/m]は、次式で与えられるものとする。

1. 0
2. 9.80×10^－5
3. 1.70×10^－4
4. 1.96×10^－4
5. 2.94×10^－4

 

 

 

 

 

　解 説　　　　

本問では3本の導体があり、全て同一条件のものとなっています。また、問われているのは各導体1m当たりに働く力の大きさF₀の値[N/m]なので、どれか1つの導体に注目して考えていけばよいことになります。

よって、今回は正三角形の一番上の頂点に注目して考えていきたいと思います(もちろん、左下や右下を選んでも構いません)。

注目した頂点に対して、求めたい力の大きさF₀と、2本の導体間に働く力の大きさFを図示すると、次のように表すことができます。

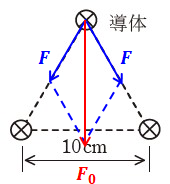
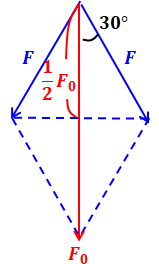
これは正三角形なので内角は60°であり、問題文にFの式と各種の数値が与えられているため、問われているF₀は以下のような計算によって求めることができます。

なお、下式において、r[m]のところは10[cm]＝0.1[m]として計算する点に注意してください。

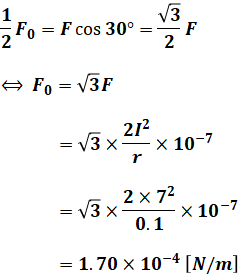
以上から、正解は(3)となります。