問 題
図のように、平行板コンデンサの上下極板に挟まれた空間の中心に、電荷Q[C]を帯びた導体球を保持し、上側極板の電位がE[V]、下側極板の電位が-E[V]となるように電圧源をつないだ。
ただし、E>0とする。同図に、二つの極板と導体球の間の電気力線の様子を示している。
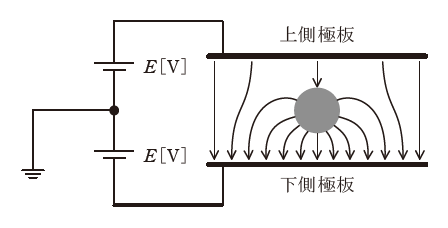
このとき、電荷Q[C]の符号と導体球の電位U[V]について、正しい記述のものを次の(1)~(5)のうちから一つ選べ。
- Q>0であり、0<U<Eである。
- Q>0であり、U=Eである。
- Q>0であり、0<E<Uである。
- Q<0であり、U<-Eである。
- Q<0であり、-E<U<0である。
正解 (1)
解 説
まず、問題文と図の条件から、上側極板の電位がE[V]、下側極板の電位が-E[V]であることがわかります。また、電気力線は正電荷(+)から負電荷(-)へ向かって延びるので、これらを図に描き込むと、次のように表すことができます。
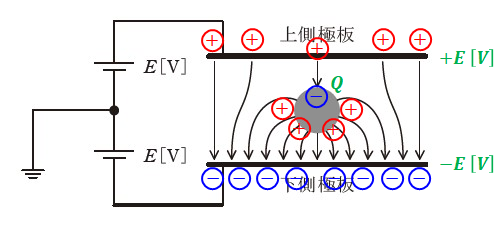
上図において、電荷Q[C]を帯びた導体球のところを見ると、電気力線が入り込む数(-)よりも出ていく数(+)のほうが多いことがわかります(inが1本、outが9本)。つまり、トータルで考えるとこの導体球は正電荷(+)の性質を持っていることになります。
よって、電荷Q[C]は「Q>0」の関係が成り立ちます。
続いて、導体球の電位Uについて考えます。上記の通り、上側極板の電位がE[V]、下側極板の電位が-E[V]であり、ちょうど真ん中の位置の電位が0[V]となります。
ここで、この導体球はトータルで正電荷(+)を帯びているため、極板間のうち上側極板のほうに寄っていることがわかります。つまり、0[V]よりもE[V]側にあるということです。ただし、少しは負電荷(-)の要素もあるので、完全にE[V]になるわけではありません。
よって、導体球の電位U[V]は「0<U<E」の範囲におさまります。
以上から、正解は(1)となります。

コメント