問 題
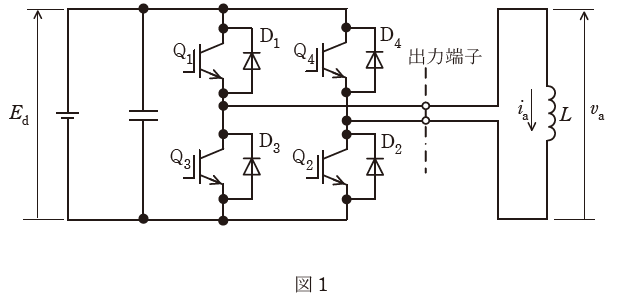
図1は、IGBTを用いた単相ブリッジ接続の電圧形インバータを示す。直流電圧Ed[V]は、一定値と見なせる。出力端子には、インダクタンスL[H]の誘導性負荷が接続されている。
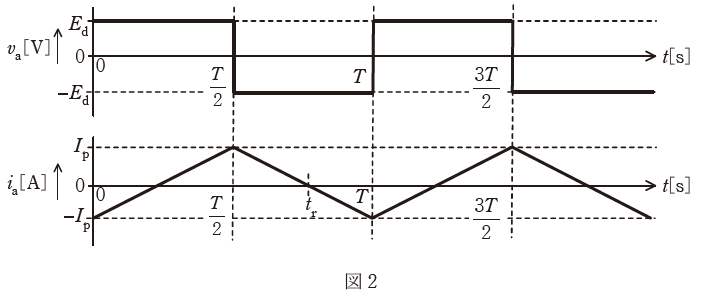
図2は、このインバータの動作波形である。時刻t=0sでIGBT Q3及びQ4のゲート信号をオフにするとともにQ1及びQ2のゲート信号をオンにすると、出力電圧vaはEd[V]となる。
t=T/2[s]でQ1及びQ2のゲート信号をオフにするとともにQ3及びQ4のゲート信号をオンにすると、出力電圧vaは-Ed[V]となる。これを周期T[s]で繰り返して方形波電圧を出力する。
このとき、次の(a)及び(b)の問に答えよ。
ただし、デバイス(IGBT及びダイオード)での電圧降下は無視するものとする。
(a) t=0sにおいてia=-Ip[A]とする。時刻t=T/2[s]の直前ではQ1及びQ2がオンしており、出力電流は直流電源からQ1→負荷→Q2の経路で流れている。
t=T/2[s]でIGBT Q1及びQ2のゲート信号をオフにするとともにQ3及びQ4のゲート信号をオンにした。
その直後(図2で、t=T/2[s]から、出力電流が0Aになるt=tr[s]までの期間)、出力電流が流れるデバイスとして、正しい組合せを次の(1)~(5)のうちから一つ選べ。
- Q1、Q2
- Q3、Q4
- D1、D2
- D3、D4
- Q3、Q4、D1、D2
(b) 図1の回路においてEd=100V、L=10mH、T=0.02sとする。t=0sにおける電流値を-Ipとして、t=T/2[s]における電流値をIpとしたとき、Ipの値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 33
- 40
- 50
- 66
- 100
解 説
(a)
問題となるのはt=T/2[s]の少しあとなので、まずはt=T/2[s]の直前の状態について確認しておきます。このときはQ1・Q2がオンでQ3・Q4がオフなので、出力電流は下図のように直流電源からQ1→負荷→Q2の経路で流れています。
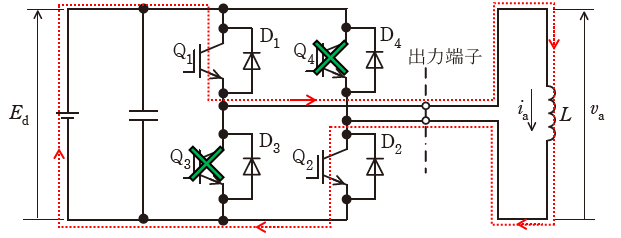
このあと、t=T/2[s]でQ3・Q4がオンでQ1・Q2がオフになりますが、しらばくの間(t=tr[s]までの期間)は問題の図2に示されている通り、出力電流iaは正のままであり、電流の流れる向きは変わりません。
このときに出力電流iaはどのデバイスを流れているのかが本問のテーマですが、以下の図を使いながら解説します。
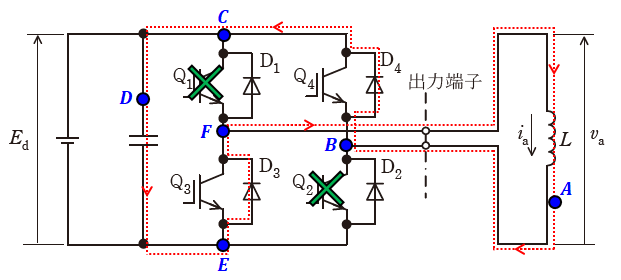
上図の点Aを始点として考えていきます。ここでの電流の向きはt=T/2[s]の直前と同じ向きなので、下向きです。
このまま進めていくと点Bに着きます。ここで進む道は上下に分岐しますが、この時点ではQ2がオフでありD2も向きが反対なので、下には進めません。よって、上に進みます。また、Q4はオンですが向きが反対なので、結局進めるのはD4のところだけです。
続いて点Cでは左か下に進めますが、Q1がオフでD1も向きが反対なので、下には進めません。よって、左に進みます。
そして点Dのコンデンサまできたところで半周分を回ったことになるので、ここからは誘導性負荷Lのある点Aまで戻る道となります。
点Eでは上か右に進めて、条件的にはどちらも通れそうです。しかし、右にいくと点Bに着いてしまい、誘導性負荷Lのある点Aに戻れません。よって、ここでは上に進みます。このとき、Q3はオンですが向きが反対なので、進めるのはD3のほうとなります。
そうすると点Fに着き、回路を1周するためには誘導性負荷Lのあるほうに向かいたいので、点Fから右に進みます。そうすると、点Aに着いて1周したことになります。
以上から、t=T/2[s]からt=tr[s]までの期間に出力電流iaが流れるデバイスはD3とD4の2つとなるので、正解は(4)です。
(b)
この問題はやや難易度の高い問題です。出題頻度からみてもそこまで重要とはいえない数式を知っておく必要があるため、ご自身の学習状況や理解度によっては後回しにしても構わないと思います。
問われているのはt=T/2[s]における電流値Ipですが、本問では出力電圧vaが不変の間でも、時間tが変われば電流iaも変化します。これは要するに、誘導性負荷に流れる電流の変化に伴って電磁誘導が起こっているということになります。
誘導性負荷によって生じる誘導起電力(=出力電圧va)は、インダクタンスL[H]、電流変化ΔI[A]、時間変化Δt[s]を用いると、次の式で表すことができます。
![]()
上式において、電流値が直線的に変化するのはt=0[S]からT/2[s]までの間なので、Δt=T/2[s]となります。また、その間に電流は-Ipから+Ipまで変化するので、ΔI=+Ip-(-Ip)=2Ipとなります。さらに、出力電圧vaは問題の図2より、va=Edです。
以上の情報と設問(b)で与えられた各数値を(1)式に代入すると、以下に示すように求めたいIpを計算することができます。
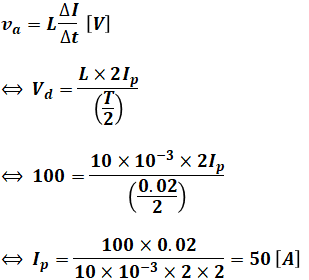
よって、正解は(3)となります。

コメント