問 題
図は、出力信号yを入力信号xに一致させるように動作するフィードバック制御系のブロック線図である。次の(a)及び(b)の問に答えよ。
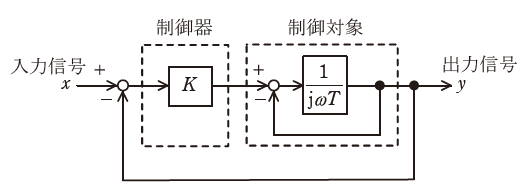
(a) 図において、K=5、T=0.1として、入力信号からフィードバック信号までの一巡伝達関数(開ループ伝達関数)を表す式を計算し、正しいものを次の(1)~(5)から一つ選べ。
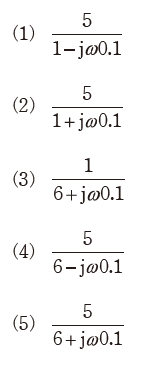
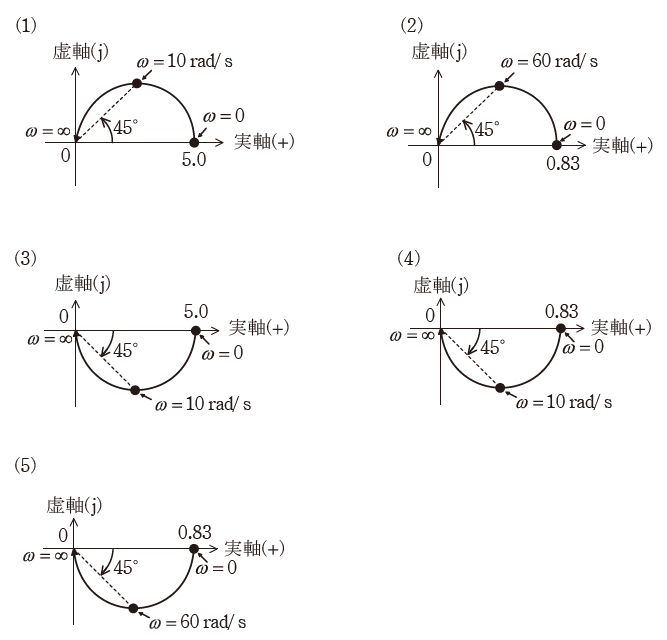
(b) (a)で求めた一巡伝達関数において、ωを変化させることで得られるベクトル軌跡はどのような曲線を描くか、最も近いものを次の(1)~(5)のうちから一つ選べ。
解 説
(a)
まず、今回は開ループ伝達関数を表す式が問われている点に注意してください。
閉ループ伝達関数が問われていれば制御系全体を式にする必要がありますが、開ループ伝達関数なら問題文にある「出力信号yを入力信号xに一致させるように動作するフィードバック制御」に相当する大枠のフィードバック部分を除き、制御器と制御対象を合わせた部分を式にすることになります。
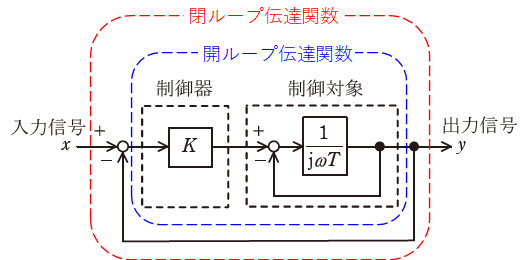
次に、上図の制御対象の枠内はフィードバックの形をしていることがわかります。フィードバックの伝達関数はブロック線図の中でも重要かつ頻出なので、ぜひ押さえておきたい内容です。
下図の左側のようなフィードバックモデルは右側のように簡略化できるので、入力をX(s)、出力をY(s)として式化すると次のようになります。これは最重要公式の一つとして覚えておいてください。なお、図中の「∓」が、式では「±」とひっくり返ることに注意が必要です。
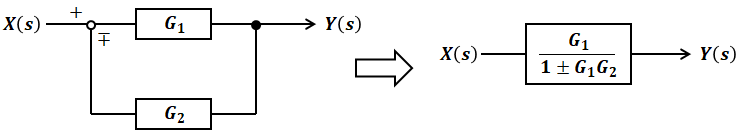
![]()
ただし今回の場合、制御対象の枠内は上記のような単純なフィードバックモデルとなっていますが、その左側に制御器が付いています。つまり、制御器と制御対象を合わせた開ループ伝達関数は次のような構成のブロック線図となります。
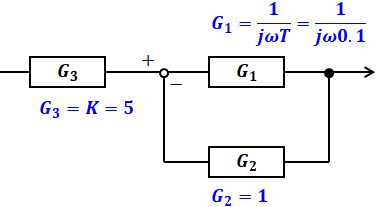
ちなみに、ブロック線図においては「1」の場合はブロックにならず、ただの線で表します。今回は上図G2がそれに当たります。
また、直列に並んだ2つのブロックをまとめると積で表すことができるため、上図のブロック線図を式にする際には、まずフィードバック部分(G1とG2)を上記で示した公式に当てはめ、その後、得られた結果にG3を掛ければよいことになります。
よって、求めたい開ループ伝達関数Gは、次のように算出することができます。

以上から、正解は(2)となります。
(b)
(a)で求めた式を図示する問題です。複素数を扱う上に変数ωが分母にあるので、一見するとグラフ化が難しいようにも感じてしまいますが、電験三種試験は5肢択一なので、このような場合は選択肢を見ながら代入法で解くと簡単に解けることが多いです。
まずは設問(a)で算出した式を再度以下に示します。
![]()
ここで、全ての選択肢にはω=0が書かれているので、試しに上式にω=0を代入して計算すると、以下のようになります。
![]()
よって、ω=0のときは実数が5、虚数が0となるので、選択肢は(1)と(3)に限られます。
続いて、選択肢(1)と(3)の目立った違いはω=10のときに虚数が正になるか負になるかなので、今度はω=10を代入していきます。すると、次のように計算できます。
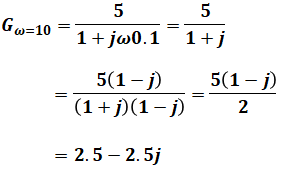
よって、ω=10のときは実数が2.5、虚数が-2.5となるので、選択肢は(3)に絞られます。実数と虚数の大きさがともに2.5なので、なす角が45°になっている点も(3)の図に矛盾しません。
以上から、正解は(3)となります。

コメント