ビル管理士試験 H27年 問86 問題と解説

　問 題　　　　　

騒音レベル83dBと92dBの騒音を合成した場合の騒音レベルとして、最も近いものは次のうちどれか。

ただし、log₁₀2=0.3010、log₁₀3=0.4771とする。

1. 85.0dB
2. 87.5dB
3. 90.0dB
4. 92.5dB
5. 95.0dB

 

 

 

 

 

　解 説　　　　　

音圧レベルを求める計算式は以下の通りです。この式を使う問題は頻出ですので、ぜひ覚えてください。

• L_B：音圧レベル [dB]
• A：基準の音の強さ [W/m²]
• B：音の強さ [W/m²]

もうひとつ知識として押さえておきたいのは、同一の騒音レベルを2つ重ねると元の騒音レベル[dB]におよそ+3されるということです。それを確かめるには、上式においてBを2Bに変えれば良いので、

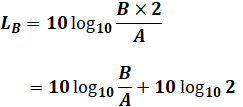
となり、また、問題文にもあるように、log₁₀2=0.3010なので、

と計算できるため、同じ騒音レベルを2つ合わせると元の騒音レベルに+3.010されることが計算で導けます。ただし、毎回この計算をしなくても、約3[dB]上がることを知識として持っておくと便利です。

ここで、この問題の話に戻ります。この問題では83[dB]と92[dB]を掛け合わせる問題ですが、この2つの差は9[dB]であり、これは3の倍数です。この手の出題は、2つの騒音レベルが一緒か、あるいは3の倍数であることが多いのがポイントとなります。

つまり、83[dB]と83[dB]を重ねると86[dB]になり、86[dB]と86[dB]を重ねると89[dB]、そして、89[dB]と89[dB]を重ねると92[dB]になるということです。よって、92[dB]というのは、正味、83[dB]を8(=2³)個分、重ねあわせたものと等価になります。

ということは、83[dB]と92[dB]とを合成するというのは、つまりは83[dB]を9(=1+8)個分、合成することになります。ここまでわかれば、先ほどの式を利用して、

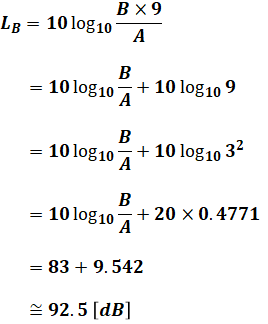
のように計算すれば、答えが出ます。