ビル管理士試験 2023年 問47 問題と解説

　問 題　　　　　

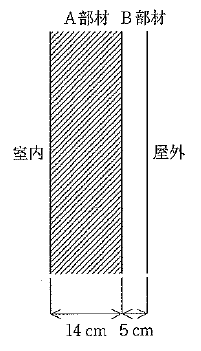
下の図のようなA部材とB部材からなる外壁がある。

いま、A部材とB部材の厚みと熱伝導率がそれぞれ14cmと1.4W/(m・K)、5cmと0.2W/(m・K)であり、室内側熱伝達率と屋外側熱伝達率がそれぞれ10W/(m²・K)、20W/(m²・K)であるとする。

室内と屋外の温度差が20℃であるとき、この外壁の単位面積当たりの熱流量として、正しいものは次のうちどれか。

1. 0.7W/m²
2. 1.4W/m²
3. 10W/m²
4. 40W/m²
5. 56W/m²

 

 

 

 

 

　解 説　　　　　

問われているのは「外壁の単位面積当たりの熱流量」ですが、このように壁を突き抜ける熱量のことを「貫流熱流」といい、次の(1)式で表されます。

• q：単位面積当たりの貫流熱流 [W/m²]
• θ：壁の内外の温度差 [K]
• R：熱貫流抵抗 [m²・K/W]

つまり、qを計算するためにはθとRを求めればよいのですが、θは問題文から20[K]と与えられています(単位が℃とKで異なりますが、温度差であれば同じことです)。よって、目下の目標はRを計算することになります。

ここで、熱が壁を通るときには100%は通過せず、ある程度のロスが発生してしまいます。どのくらい熱が遮られるのか(熱損失が大きいのか)を表すパラメータが、この熱貫流抵抗Rです。

問題の図には「室内側」、「A部材」、「B部材」、「屋外側」の4つのエリアに分かれていますが、それぞれの熱抵抗の和が熱貫流抵抗R[m²・K/W]となります。

「室内側」と「屋外側」では、熱伝達率[W/(m²・K)]の値が与えられています。単位を見るとわかるように、熱伝達率と熱抵抗とは逆数の関係があります。

一方、「A部材」と「B部材」では、部材の厚み[cm]と熱伝導率[W/(m・K)]が与えられています。これも単位に注目すると、厚みを熱伝導率で割った値が熱抵抗に相当します。ただし、[cm]は[m]に直してから計算を進めてください。

以上を踏まえると、熱貫流抵抗Rは次の(2)式のように計算することができます。

(ちょっと脱線)

問題文では、A部材とB部材には「熱伝導」という言葉が、室内側と屋外側には「熱伝達」という言葉が使われています。これは、部材のような固体の中を熱が伝わることを「熱伝導」といい、空気と壁の間のように気体と固体の間を熱が伝わることを「熱伝達」ということに由来します。

熱伝導抵抗の逆数は熱伝導率、熱伝達抵抗の逆数は熱伝達率…というのが正しい考え方ですが、どちらも同じ単位で並列に並べて計算できるので、ビル管理士の試験対策としては特に区別して覚える必要はないと思います。

(脱線おわり)

以上から、(2)式の結果を(1)式に代入すると、以下のように貫流熱流qを計算することができます。

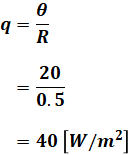
よって、外壁の単位面積当たりの熱流量は40[W]となるので、正解は(4)です。